Heap
The (binary) heap data structure is an array object that we can view as a nearly complete binary tree
Each node of the tree corresponds to an element of the array
The tree is completely filled on all levels except possibly the lowest
- which is filled from the left up to a point
An array
Athat represents a heap is an object with two attributes:A.lengthgives the number of elements in the arrayA.heap-sizerepresents how many elements in the heap are stored within arrayA- only elements in
A[1 .. A.heap-size]- where
0 ≤ A.heap-size ≤ A.lengthare valid elements of the heap
- where
- The root of the tree is
A[1] - given the index i of a node
- we can easily compute the indices of its parent, left child, and right child:
- Parent:
i/2 - Left:
2i - Right:
2i + 1
- Parent:
- we can easily compute the indices of its parent, left child, and right child:
There are two kinds of binary heaps
- max-heaps and min-heaps
- In both kinds, the values in the nodes satisfy a heap property, the specifics of which depend on the kind of heap
- In a max-heap, the max-heap property is that for every node i other than the root:
A[Parent(i)] ≥ A[i]- max hip has the largest root node and the heap goes down
- the largest element in a max-heap is stored at the root
- the subtree rooted at a node contains values no larger than that contained at the node itself
- A min-heap is organized in the opposite way
- min has a minimum root node and goes up
- the min-heap property is that for every node i other than the root:
A[Parent(i)] ≤ A[i] - The smallest element in a min-heap is at the root
- For the heap sort algorithm, we use max-heaps
- Min-heaps commonly implement
priority queues
example
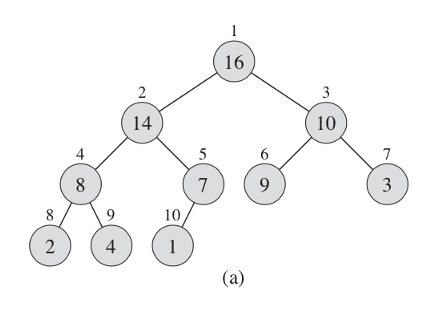
- an array that we can represent as a tree
- the numbers above the element in the array and the heap are the same, you can see how they are substituted into the leaves
- It doesn't have to be an array, different programming languages have different data structures
- it is more convenient to consider it as an array
- Array
A, which represents the heap- it also has attributes such as
length- the number of elements in the array - And
heap-size, the number of elements in the heap - The root of the tree is the first element in the array
- it also has attributes such as
function maxHeapify(A, i) {
let l = left(i);
let r = right(i);
if (l <= A.heapSize && A[l] > A[i]) {
largest = l;
} else {
largest = i;
}
if (r <= A.heapSize && A[r] > A[largest]) {
largest = r;
}
if (largest != i) {
// exchange A[i] with A[largest]
[A[i], A[largest]] = [A[largest], A[i]];
maxHeapify(A[largest]);
}
}
Maintaining the Heap Property
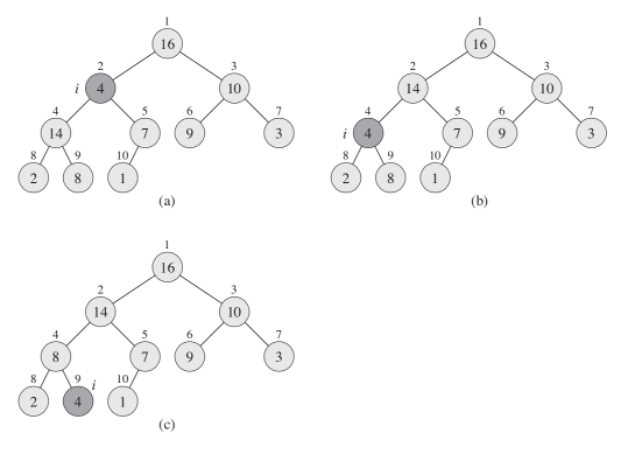
In order to maintain the max-heap property, we call the function maxHeapify
- When it is called, maxHeapify assumes that the binary trees rooted at left(i) and right(i) are max-heaps
- but that A[i] might be smaller than its children, thus violating the max-heap property
- Function maxHeapify lets the value at
A[i]"float down" in the max-heap so that the subtree rooted at index i obeys the max-heap property
- When it is called, maxHeapify assumes that the binary trees rooted at left(i) and right(i) are max-heaps
example
- heap must somehow support itself
- when inserting or when deleting elements a heap rebuild should take place
- this procedure can be called as
maxHeapify- When it is called, we assume that the left and right nodes are also maxHeap
- these nodes can be smaller than its children, and we have to let it go down below
- the second element has ceased to meet the requirement, and we check the left heap until we reach the sheet
- At each step, the largest of the elements
A[i],A[left(i)], andA[right(i)]is determined, and its index is stored in largest - If
A[i]is largest, then the subtree rooted at node i is already a max-heap and the procedure terminates - Otherwise, one of the two children has the largest element, and
A[i]is swapped withA[largest], which causes node i and its children to satisfy the max-heap property - The node indexed by largest, however, now has the original value
A[i], and thus the subtree rooted at largest might violate the max-heap property - Consequently, we call maxHeapify recursively on that subtree
- The running time of maxHeapify on a subtree of size n rooted at a given node i is the
Θ(1)time to fix up the relationships among the elementsA[i],A[left(i)], andA[right(i)] - plus the time to run maxHeapify on a subtree rooted at one of the children of node i (assuming that the recursive call occurs)
- The children's subtrees each have size at most
2n/3 - the worst case occurs when the bottom level of the tree is exactly half full—and therefore we can describe the running time of maxHeapify by the recurrence:
O(log n)
- this procedure can be called as
- when inserting or when deleting elements a heap rebuild should take place
- heap must somehow support itself
Building a Heap
- The heap should be built using method
buildMaxHeap- To do this, need to run the entire array through the maxHeapify function
- the complexity becomes
O(n log n)- have a linear dependency as it applies a function for each element and call maxHeapify itself
- We can use the procedure maxHeapify in a bottom-up manner to convert an array
A[1..n], wheren = A.length, into a max-heap - The elements in the subarray
A[(n/2+1)..n]are all leaves of the tree, and so each is a 1-element heap to begin with - The function buildMaxHeap goes through the remaining nodes of the tree and runs maxHeapify on each one
- We can compute a simple upper bound on the running time of buildMaxHeap
- Each call to maxHeapify costs O(lgn) time
- Procedure buildMaxHeap makes
O(n)calls - the running time is
O(n log n)- This upper bound, though correct, is not asymptotically tight