Graphs

• All types of trees are special cases of graphs
• a collection of nodes or values called vertices that might be related
  • relations between vertices are called edges
  • G = (V, E)
• many things in life can be represented by graphs
  • e.g. a social network can be represented by a graph whose vertices are users and whose edges are friendships between the users
  • similarly, a city map can be represented by a graph whose vertices are locations in the city and whose edges are roads between the locations
• typically, we represent a graph as an adjacency list
  • |V|
  • it can store a list of nodes in the graph
    • every node stores value and a list of it's edges (or a list of it's adjacencies)
• a graph can also be represented by a 2 dimensional array

Graph cycle

• a cycle occurs in a graph when 3 or more vertices in the graph are connected so as to form a closed loop
• note that the definition of a graph cycle is sometimes broadened to include cycles of length 2 or 1
  • in the context of coding interviews, when dealing with questions that involve graph cycles
    • it's important to clarify what exactly constitutes a cycle

Acyclic Graph

• a graph that has no cycles

Cyclic Graph

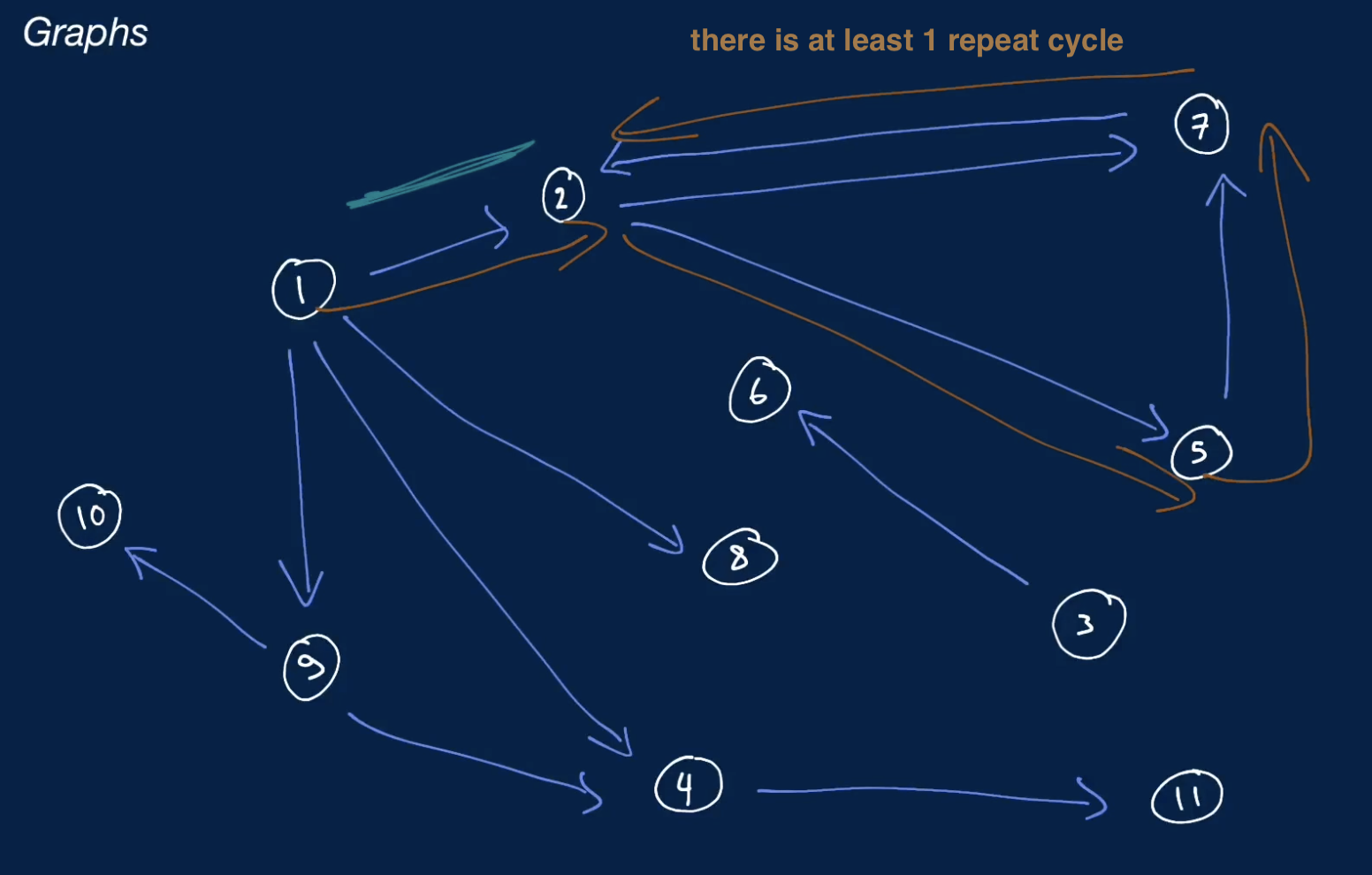
• a graph that has at least 1 cycle
• if you are traversing through the graph, and going down connections, and found yourself revisiting a connection that you have previously visited just by following the path of 3 edges
  • then that means there's a cycle in the graph

Directed Graph

• a graph that whose edges are directed
  • meaning that they can only be traversed in 1 direction, which is specified
• for e.g. a graph of airports and flights would likely be directed
  • since a flight specifically goes from 1 airport to another (has a direction)
    • without necessarily implying the presence of a flight in the opposite direction

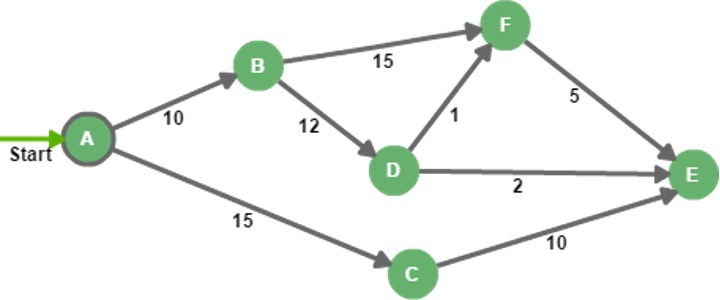
Directed Graph with Weights

Undirected Graph

• a graph whose edges are undirected, meaning that they can be traversed in both directions
• e.g. a graph of friends would likely be undirected, since friendship is by nature bidirectional

Connected Graph

• a graph is connected if for every pair of vertices in the graph there's a path of 1 or more edges connecting the given vertices
• in the case of a directed graph, the graph is
  • strongly connected if there are bidirectional connections between the vertices of every pair of vertices
    • for every vertex-pair (u, v), can reach v from u and u from v
  • weakly connected if there are connections (but not necessarily bidirectional ones) between the vertices of every pair of vertices

Disconnected Graph

• a graph that isn't connected is said to be disconnected

standard operations and complexities

Storing a graph: O(V + E) space

• storing V vertices (nodes)
  • V is the number of vertices in the graph
• storing E edges
  • E is the number of edges in the graph

Traversing a graph: O(V + E) time

Depth First Search (DFS)

• traversing the graph deeper before going wide

Breath First Search (BFS)

• traversing the graph wider before going deep

• it is one of the simplest algorithms for searching a graph and the archetype for many important graph algorithms

• The algorithm works on both directed and undirected graphs

• example: assumes that the input graph G = (V, E) is represented using adjacency lists

  function BFS(Graph, source) {
    let u, vertex;
  
    for (u of Graph) {
      u.color = "WHITE";
      u.dist = Number.POSITIVE_INFINITY;
      u.parent = null;
    }
  
    source.color = "GRAY";
    source.dist = 0;
    source.parent = null;
    Queue = [];
    Queue.push(source);
  
    while (Queue.length > 0) {
      u = Queue.unshift();
  
      for (vertex of Graph.Adj[u]) {
        if (vertex.color === "WHITE") {
          vertex.color = "GRAY";
          vertex.dist = u.dist + 1;
          vertex.parent = u;
          Queue.push(Queue, vertex);
        }
      }
  
      u.color = "BLACK";
    }
  }