Trees
- a special type of graph
- trees excel at storing data hierarchically and are commonly used as a means of testing your knowledge of recursion during coding interviews
- it is a data structure that consists of nodes, each with some value and pointers to child-nodes
- which recursively form subtrees in the tree
- the 1st node in a tree is referred to as the root of the tree
- while the nodes at the bottom of a tree (the nodes with no child-nodes) are referred to as leaf nodes or leaves
- the paths between the root of a tree and its leaves are called branches
- the height of a tree is the length of its longest branch
- the depth of a tree node is its distance from its tree's root
- also known as the node's level in the tree
- a tree is effectively a graph that's connected, directed, and acyclic
- has an explicit root node, and whose nodes all have a single parent (except for the root node)
- in most implementations of trees, tree nodes don't have a pointer to their parent, but can if desired
Types of trees
Binary Trees
- the root node has 2 child nodes
- every other nodes have up to 2 child nodes
- the structure of a binary tree is such that many of its operations have a logarithmic time complexity, making binary tree a commonly used data structure
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class Node<T> {
constructor(public value: T) {
this.value = value;
this.left = null;
this.right = null;
}
}
Binary Search Tree (BST)
it is a node-based binary tree data structure which has the following properties
- The left subtree of a node contains only nodes with values smaller than the node's value
- The right subtree of a node contains only nodes with values bigger than the node's value
- The left and right subtree each must also be a binary search tree or be null
If a node is to be inserted into a tree, it is compared with current node (starting from the root)
- If the node's value is less than current, we send it down to left subtree
- If node's value is greater than or equal to current
- it is sent to the right subtree
- This process is repeated for each encountered node
K-ary Tree
- a tree where every node (including the root) have up to k child nodes
- e.g.: a binary tree is a k-ary tree where k === 2
Perfect Binary Tree
- a binary tree whose interior nodes all have 2 child nodes and whose leaf nodes all have the same depth
1
/ \
2 3
/ \ / \
4 5 6 7
/\ /\ /\ /\
8 9 10 11 12 13 14 15
Complete Binary Tree
- a binary tree that's almost perfect
- its interior nodes all have 2 child nodes
- but its leaf nodes don't necessarily all have the same depth
- furthermore, the nodes in the last level of a complete binary tree are as far left as possible
1
/ \
2 3
/ \ / \
4 5 6 7
/\
8 9 - a binary tree is incomplete if the nodes in its last level aren't as far left as possible
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Balanced Binary Tree
1
/ \
2 3
/ \ / \
4 5 6 7
/ \ /
10 9 8
- a binary tree whose nodes all have left and right subtrees whose heights differ by no more than 1
- a balanced binary tree is such that the logarithmic time complexity
O(log n)of its operations is maintained - e.g.: inserting a node at the bottom of the following imbalanced binary tree's left subtree would clearly not be a logarithmic-time operation, since it would involve traversing through most of the tree's nodes
1
/ \
2 3
/
4
/
8
/
10
Full Binary Tree
- a binary tree whose nodes all have either 2 child nodes or 0 child nodes
1
/ \
2 3
/ \
6 7
/ \
8 9
Heaps
- they are typically binary heaps
- a special type of binary trees, where every node in the tree satisfies the min or max heap property
Min Heaps
Max Heaps
Ternary Tree
- the root node has 3 child nodes
- every other nodes have up to 3 child nodes
Tries
- a tree like data structure that typically stores characters in a string
AVL Trees
- able to rebalance themselves to obtain the log N complexity
Red Black Trees
- able to rebalance themselves to obtain the log N complexity
standard operations and complexities
Storing all types of tree: O(N) space
- N is the total number of nodes in the tree
Traversing through the entire tree: O(N) time
Traversing 1 subtree at every step for a balance binary tree: O(log N) time on average
- if the tree is skewed, it becomes O(N) time on worst
Search, Insert, Delete
- for Binary Search Tree:
O(h)- h is the height of the BST
- for skewed tree:
O(n)- n is the number of nodes
Traversal Types
- Using Recursion
| pros | cons |
|---|---|
| The code may be easier to write | Recursive functions are generally slower than non-recursive function |
| To solve such problems which are naturally recursive such as tower of Hanoi | It may require a lot of memory space to hold intermediate results on the system stacks |
| Reduce unnecessary calling of function | Hard to analyze or understand the code |
| Extremely useful when applying the same solution | It is not more efficient in terms of space and time complexity |
| Recursion reduce the length of code | The computer may run out of memory if the recursive calls are not properly checked |
| It is very useful in solving the data structure problem | |
| Stacks evolutions and infix, prefix, postfix evaluations etc |
Breath First Traversal
Depth First Traversal
Inorder (Left, Root, Right)
- example
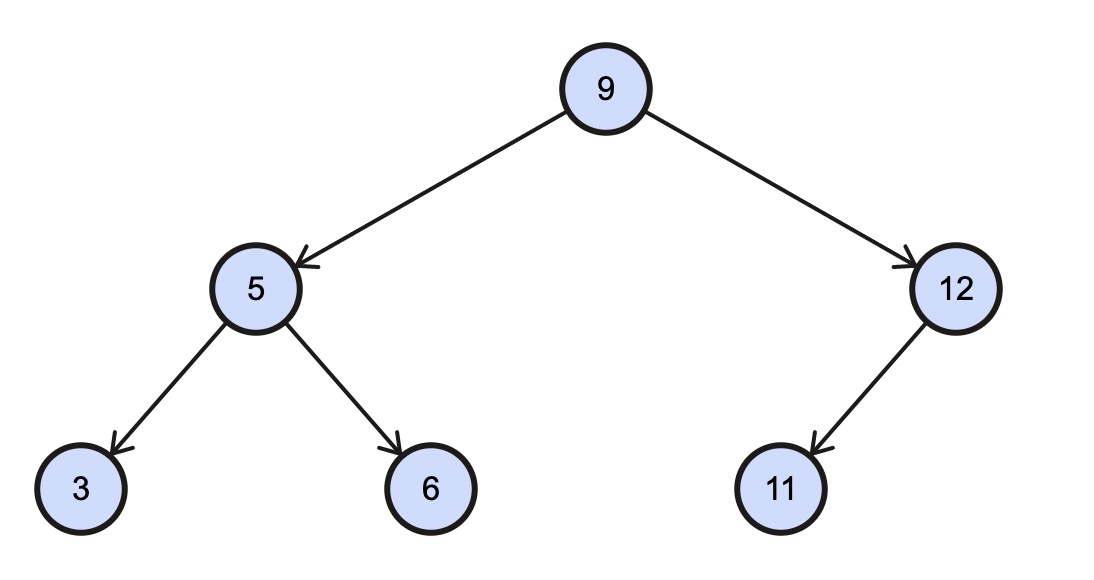
- 3, 5, 6, 9, 11, 12
- prints the values in the left subtree, then the value of the root subtree, then the right subtree
- Traverse the left subtree, i.e., call Inorder(left-subtree)
- Visit the root.
- Traverse the right subtree, i.e., call Inorder(right-subtree)
def in_order(current_node):
if current_node:
in_order(current_node.left)
print(current_node.value)
in_order(current_node.right)
function inOrder(node: Node | null) {
if (node) {
inOrder(node.left);
console.log(node.value);
inOrder(node.right);
}
}
def in_order(root):
if root is None:
return
node_stack = []
node_stack.append(root)
while(len(node_stack) > 0):
current_node = node_stack.pop()
# Note that right child is pushed first so that left is processed first
if current_node.right:
node_stack.append(current_node.right)
print(current_node.value)
if current_node.left:
node_stack.append(current_node.left)
Preorder (Root, Left, Right)
- example
- 9, 5, 3, 6, 12, 11
- prints the root value, then value in left subtree, then value in right subtree
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left-subtree)
- Traverse the right subtree, i.e., call Preorder(right-subtree)
def pre_order(current_node):
if current_node:
print(current_node.value)
pre_order(current_node.left)
pre_order(current_node.right)
function preOrder(node: Node | null) {
if (node) {
console.log(node.value);
preOrder(node.left);
preOrder(node.right);
}
}
def pre_order(root):
if root is None:
return
node_stack = []
node_stack.append(root)
while(len(node_stack) > 0):
current = node_stack.pop()
print(current.value)
# Note that right child is pushed first so that left is processed first
if current.right:
node_stack.append(current.right)
if current.left:
node_stack.append(current.left)
Postorder (Left, Right, Root)
- example
- 3, 6, 5, 11, 12, 9
- prints the value of the left subtree, then the value of the right subtree, then the root value
- Traverse the left subtree, i.e., call Postorder(left-subtree)
- Traverse the right subtree, i.e., call Postorder(right-subtree)
- Visit the root.
def post_order(current_node):
if current_node:
post_order(current_node.left)
post_order(current_node.right)
print(current_node.value)
function postOrder(node: TreeNode | null) {
if (node) {
postOrder(node.left);
postOrder(node.right);
console.log(node.value);
}
}
def post_order(root):
if root is None:
return
node_stack = []
node_stack.append(root)
while(len(node_stack) > 0):
current = node_stack.pop()
# Note that right child is pushed first so that left is processed first
if current.right:
node_stack.append(current.right)
if current.left:
node_stack.append(current.left)
print(current.value)
Binary Search
def binary_search(current, target):
if current is None:
return None
if current.value == target:
return current
if target > current.value:
return binary_search(current.right, target)
if target < current.value:
return binary_search(current.left, target)
return None
function binarySearch(current: Node | null, target: number): Node | null {
if (current === null) {
return null;
}
if (target === current.value) {
return current;
}
if (target > current.value) {
return binarySearch(current.right, target);
}
if (target < current.value) {
return binarySearch(current.left, target);
}
return null;
}
def binary_search(tree, target):
current = tree
while current:
if current.value == target:
return current.value
if target > current.value:
current = current.right
elif target < current.value:
current = current.left
else:
break
return None
Min and Max of Binary Search Trees
Min
- value is a minimum by following left child pointers from the root until we encounter a null
function treeMinimum(node: Node) {
while (node.left) {
node = node.left;
}
return node;
}
Max
- value is a maximum by following right child pointers from the root until we encounter a null
function treeMaximum(node: Node) {
while (node.right) {
node = node.right;
}
return node;
}
Successor
- it is the node with the smallest value greater than targetNode.value
function getSuccessor(tree: Node, targetNode: Node) {
if (tree === targetNode) {
return null;
}
if (targetNode.right) {
return treeMinimum(targetNode.right);
}
let successor = null;
let currentNode: Node | null = tree;
while (currentNode) {
if (currentNode.value <= targetNode.value) {
currentNode = currentNode.right;
} else {
successor = currentNode;
currentNode = currentNode.left;
}
}
return successor;
}
Insertions
function insertNode(tree: Node | null, node: Node) {
if (!tree) {
return node;
}
let leafNode: Node | null = tree;
let leafNodeParent: Node = tree;
while (leafNode) {
leafNodeParent = leafNode;
leafNode = node.value < leafNode.value ? leafNode.left : leafNode.right;
}
if (node.value < leafNodeParent.value) {
leafNodeParent.left = node;
} else {
leafNodeParent.right = node;
}
}
Deletion
The overall strategy for deleting a node node from a binary search tree tree has three basic cases
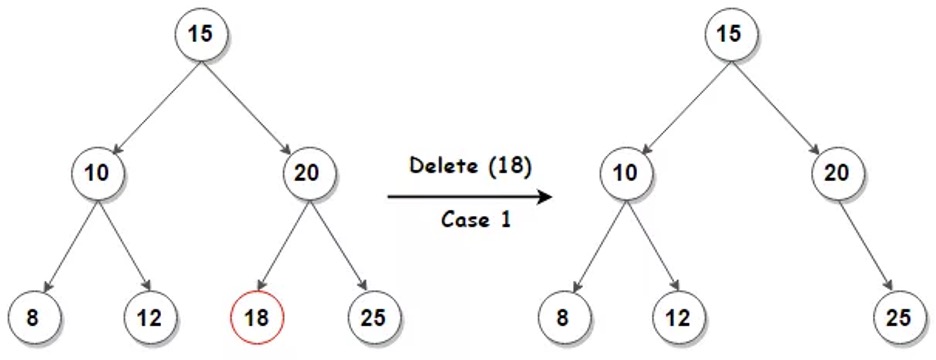
If node is leaf (has no children)
- then remove it by modifying its parent to replace node with null as its child
If node has just one child
- then elevate that child to take nodes position in the tree by modifying node parent to replace node by nodes child
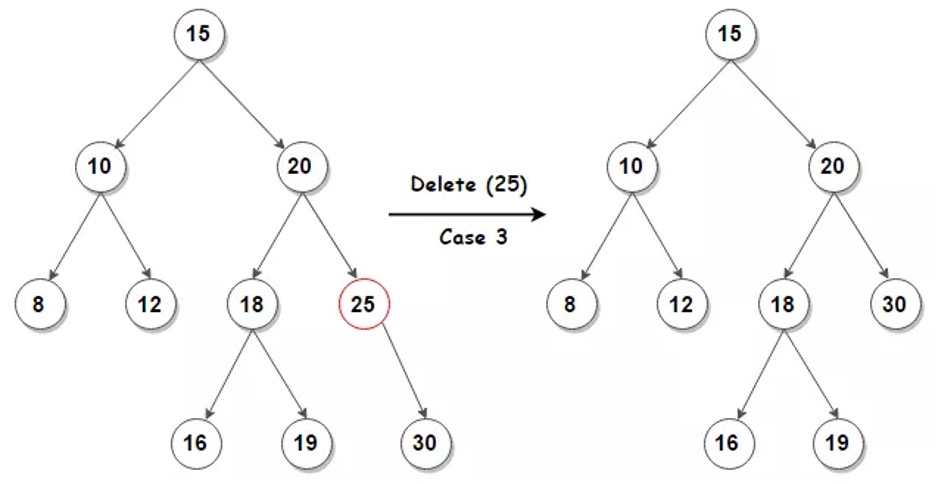
If node has two children
- then find node successor parent
- must be in node right subtree
- and have parent take nodes position in the tree
- The rest of nodes original right subtree becomes parents new right subtree, and nodes left subtree becomes parents new left subtree
- This case is the tricky because it matters whether parent is nodes right child
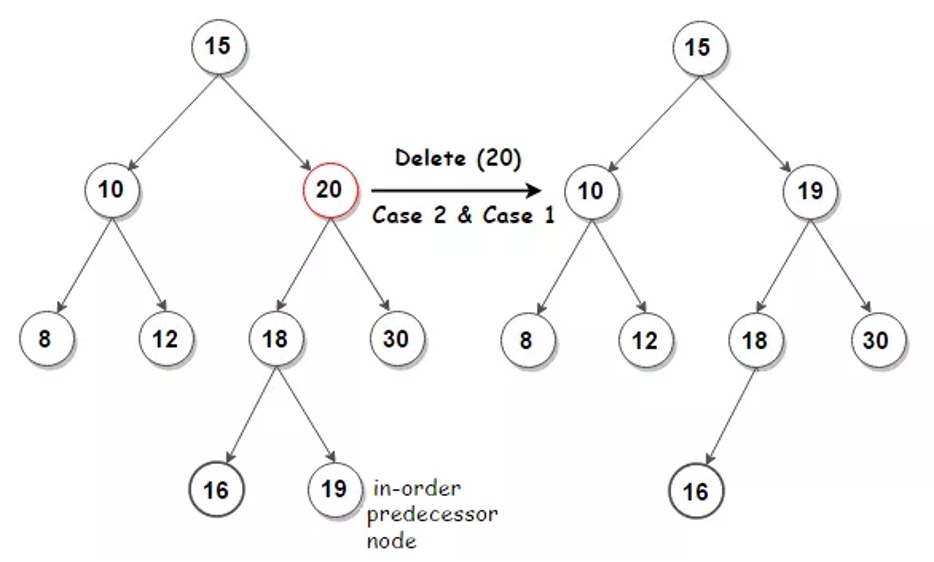
- then find node successor parent
function deleteNode(tree: Node | null, value: number): Node | null {
if (tree === null) {
return tree;
}
if (value < tree.value) {
tree.left = deleteNode(tree.left, value);
} else if (value > tree.value) {
tree.right = deleteNode(tree.right, value);
}
// this is the node to be deleted
else {
// node with only one child or no child
if (tree.left === null) {
return tree.right;
}
if (tree.right === null) {
return tree.left;
}
// node with two children: get the inorder predecessor (largest in the left subtree)
tree.value = treeMaximum(tree.left).value;
// delete the inorder predecessor
tree.left = deleteNode(tree.left, tree.value);
}
return tree;
}
full Binary Search Tree example
utils
enum Compare {
LessThan = -1,
BiggerThan = 1,
Equals = 0,
}
function compare<T>(a: T, b: T): number {
if (a === b) {
return Compare.Equals;
}
return a < b ? Compare.LessThan : Compare.BiggerThan;
}
export class Node<T> {
public left: Node<T> = null;
public right: Node<T> = null;
constructor(public value: T) {
this.value = value;
}
public toString() {
return `${this.value}`;
}
}class BinarySearchTree<T> {
protected root: Node<T> = null;
/**
* @description: insert element
*/
public insert(value: T) {
if (this.root === null) {
// edge case: insert into root node
this.root = new Node(value);
} else {
// recursively find the insertion position
this.insertNode(this.root, value);
}
}
/**
* @description: recursive insertion method
*/
protected insertNode(node: Node<T>, value: T) {
if (compare(value, node.value) === Compare.LessThan) {
// If the value is smaller than node.value, go to the left
if (node.left === null) {
// Baseline condition: the left side is empty and directly assigned
node.left = new Node(value);
} else {
// otherwise recurse
this.insertNode(node.left, value);
}
// If the value is larger than node.value, go to the right
} else if (node.right === null) {
// Baseline condition: the right side is empty and directly assigned
node.right = new Node(value);
} else {
// otherwise recurse
this.insertNode(node.right, value);
}
}
/**
* @description: return the root node
*/
public getRoot() {
return this.root;
}
/**
* @description: search element
*/
public search(value: T) {
// call recursive search element method
return this.searchNode(this.root, value);
}
/**
* @description: recursive search element method
*/
private searchNode(node: Node<T>, value: T): boolean {
// Baseline condition: return false when null is found
if (node === null) {
return false;
}
if (compare(value, node.value) === Compare.LessThan) {
// value is smaller than node.value, look left
return this.searchNode(node.left, value);
} else if (compare(value, node.value) === Compare.BiggerThan) {
// value is bigger than node.value, look right
return this.searchNode(node.right, value);
}
// value is equal to node.value, element is found
return true;
}
public inOrderTraverse(callback: Function) {
this.inOrderTraverseNode(this.root, callback);
}
private inOrderTraverseNode(node: Node<T>, callback: Function) {
if (node !== null) {
this.inOrderTraverseNode(node.left, callback);
callback(node.value);
this.inOrderTraverseNode(node.right, callback);
}
}
public preOrderTraverse(callback: Function) {
this.preOrderTraverseNode(this.root, callback);
}
private preOrderTraverseNode(node: Node<T>, callback: Function) {
if (node !== null) {
callback(node.value);
this.preOrderTraverseNode(node.left, callback);
this.preOrderTraverseNode(node.right, callback);
}
}
postOrderTraverse(callback: Function) {
this.postOrderTraverseNode(this.root, callback);
}
private postOrderTraverseNode(node: Node<T>, callback: Function) {
if (node !== null) {
this.postOrderTraverseNode(node.left, callback);
this.postOrderTraverseNode(node.right, callback);
callback(node.value);
}
}
/**
* @description: return smallest element in tree
*/
public min() {
// call iterator method
return this.minNode(this.root);
}
/**
* @description: returns the smallest element under the specified subtree
*/
protected minNode(node: Node<T>) {
let current = node;
// keep looking left
while (current !== null && current.left !== null) {
current = current.left;
}
return current;
}
/**
* @description: return largest element in tree
*/
public max() {
// call iterator method
return this.maxNode(this.root);
}
/**
* @description: returns the largest element under the specified subtree
*/
protected maxNode(node: Node<T>) {
let current = node;
// keep looking right
while (current !== null && current.right !== null) {
current = current.right;
}
return current;
}
/**
* @description: remove the specified element
*/
public remove(value: T) {
// Call the recursive method, the recursion here is special, and the deleted tree will be returned
this.root = this.removeNode(this.root, value);
}
/**
* @description: A recursive method that removes the specified element in the specified subtree. After each processing, the processed node needs to be returned to this node
*/
protected removeNode(node: Node<T>, value: T) {
// baseline condition
if (node === null) {
return null;
}
if (compare(value, node.value) === Compare.LessThan) {
// When the value is less than node.value, look left
node.left = this.removeNode(node.left, value);
return node;
} else if (compare(value, node.value) === Compare.BiggerThan) {
// When the value is greater than node.value, look to the right
node.right = this.removeNode(node.right, value);
return node;
} else {
// value is equal to node.value
// At this point, the node to be deleted has been found
// handle 3 special conditions
// case 1: When the node to be deleted is a leaf node
if (node.left === null && node.right === null) {
node = null;
return node;
}
// case 2: When the node to delete has only one right child
if (node.left === null) {
node = node.right;
return node;
// The same deleted node has only one left child node
} else if (node.right === null) {
node = node.left;
return node;
}
// case 3: When the node to be deleted has two children
const aux = this.minNode(node.right);
node.value = aux.value;
node.right = this.removeNode(node.right, aux.value);
return node;
}
}
}let tree = new BinarySearchTree<number>();
console.log(tree.getRoot());
tree.insert(11);
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
console.log(tree.getRoot());
console.log(tree.getRoot().left);
console.log(tree.getRoot().right);
tree.preOrderTraverse(console.log);
tree.inOrderTraverse(console.log);
tree.postOrderTraverse(console.log);
console.log(tree.search(8));
console.log(tree.search(0));
console.log(tree.min());
console.log(tree.max());
console.log(tree.remove(8));
console.log(tree.search(8));