Big O Notation

• the speed and memory usage of an algorithm aren't necessarily fixed
  • they might change depending on the input
• it is a powerful tool that allow us to generalize the space-time complexity of an algorithm as a function of its input size
• variables used in Big O notation denote the sizes of inputs to algorithms
  • e.g.: O(n) might be the time complexity of an algorithm that traverses through an array of length n
  • similarly, O(n + m) might be the time complexity of an algorithm that traverses through an array of length n and through a string of length m
• not that in the context of coding interviews, Big O notation is usually understood to describe the worst-case complexity of an algorithm
  • even though the worst case complexity might differ from the average-case complexity
  • e.g.: some sorting algorithms have different time complexities depending on the layout of elements in their input array
    • in rare cases, their time complexity will be much worse than in more common cases
    • similarly, an algorithm that takes in a string and performs special operations on uppercase characters might have a different time complexity when run on a input string of only uppercase characters vs on an input string with just a few uppercase characters

common complexities and their Big O notations ordered from fastest to slowest

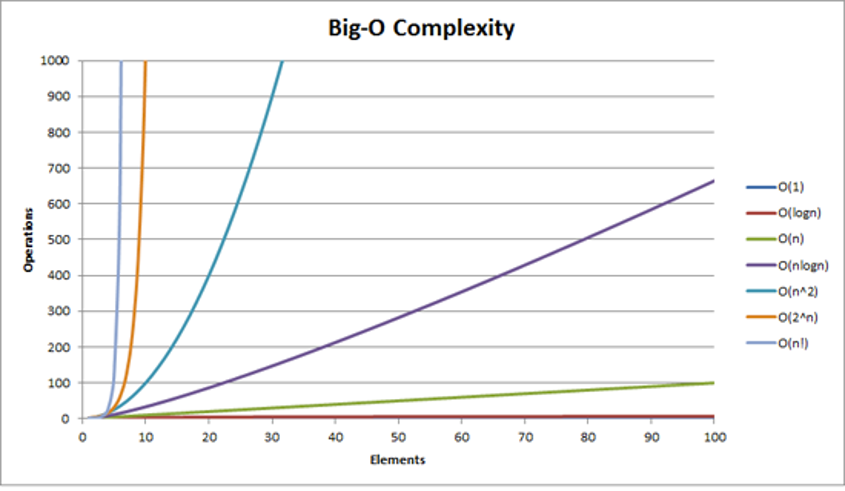
Constant: O(1)

Logarithmic: O(log n)

Linear: O(n)

• do not join them together if the input value are from a different source
  • O(n + m)

Log-linear: O(n log n)

Quadratic: O(n²)

• drop the smaller unit if the input value are from the same source
  • O(n² + n) = O(n²)
• do not drop the smaller unit if the input value are from a different source
• O(n² + 2m) = O(n² + m)

Cubic: O(n³)

Exponential: O(2ⁿ)

Factorial: O(n!)

4! = 4 3 2 * 1 = 24