Divide & Conquer

• We can choose from a wide range of algorithm design techniques

  • For insertion sort, we used an incremental approach
    • having sorted the subarray A[1 .. j-1], we inserted the single element A[j] into its proper place, yielding the sorted subarray A[1 .. j]

• an alternative design approach, known as divide-and-conquer

  • We use divide-and-conquer to design a sorting algorithm
    • whose worst-case running time is much less than that of insertion sort
    • One advantage of divide-and-conquer algorithms is that their running times are often easily determined

• Many useful algorithms are recursive in structure

  • to solve a given problem, they call themselves recursively one or more times to deal with closely related sub-problems
  • These algorithms typically follow a divide-and-conquer approach
    • they break the problem into several subproblems that are similar to the original problem but smaller
    • solve the subproblems recursively
    • then combine these solutions to create a solution to the original problem

  

algorithm

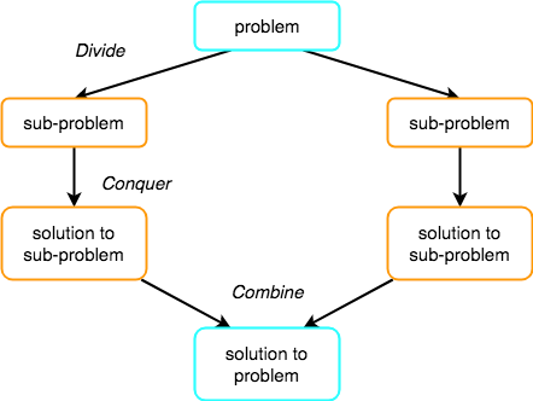
• The divide-and-conquer paradigm involves 3 steps at each level of the recursion

  1. Divide the problem into a number of subproblems that are smaller instances of the same problem
  2. Conquer the subproblems by solving them recursively
     • If the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner
  3. Combine the solutions to the subproblems into the solution for the original problem

• another method of explanation

  1. Divide problem into several smaller subproblems
     • normally, the subproblems are similar to the original
  2. Conquer the subproblems by solving them recursively
     • base case: solve small enough problems by brute force
  3. Combine the solutions to get a solution to the subproblems
     • and finally a solution to the original problem
  4. Divide and Conquer algorithms are normally recursive