Red-Black Tree

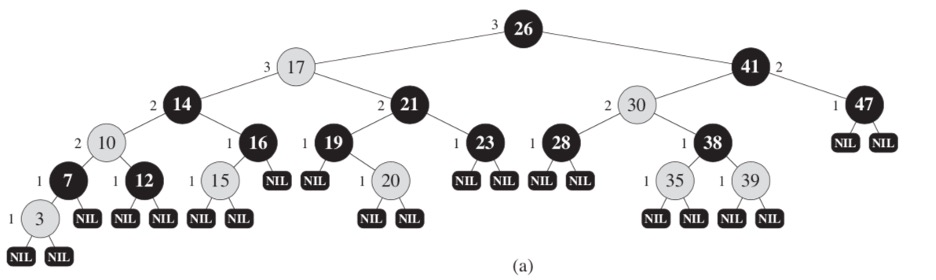
• it is a self-balancing binary search tree with one extra bit of storage per node
  • its color can be either RED or BLACK
  • By constraining the node colors on any simple path from the root to a leaf
    • red-black trees ensure that no such path is more than twice as long as any other, so that the tree is approximately balanced
• Each node of the tree contains the attributes
  • color, value, left, right, and parent
• If a child or the parent of a node does not exist, the corresponding pointer attribute of the node contains the value null
  • We regard these nulls as being pointers to leaves (external nodes) of the binary search tree and the normal, key-bearing nodes as being internal nodes of the tree
• it is a binary tree that satisfies the following red-black properties
  1. Every node is either red or black
  2. The root is black
  3. all leaf node are black
  4. If a node is red, then both its children and parent are black
  5. Every path from a node (including root) to any of its descendants NULL nodes has the same number of black nodes
• it also has a lemma
  • a tree with n internal nodes has height at most 2log (n + 1)

Why Red-Black Trees?

• Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST
• The cost of these operations may become O(n) for a skewed Binary tree
• If we make sure that the height of the tree remains O(log n) after every insertion and deletion
  • then we can guarantee an upper bound of O(log n) for all these operations
• The height of a Red-Black tree is always O(log n) where n is the number of nodes in the tree

Method	Time Complexity
Search	O(log n)
Insert	O(log n)
Delete	O(log n)

Comparison with AVL Tree

• The AVL trees are more balanced compared to Red-Black Trees
  • but they may cause more rotations during insertion and deletion
• if the application involves frequent insertions and deletions
  • then Red-Black trees should be preferred
• if the insertions and deletions are less frequent and search is a more frequent operation
  • then AVL tree should be preferred over the Red-Black Tree

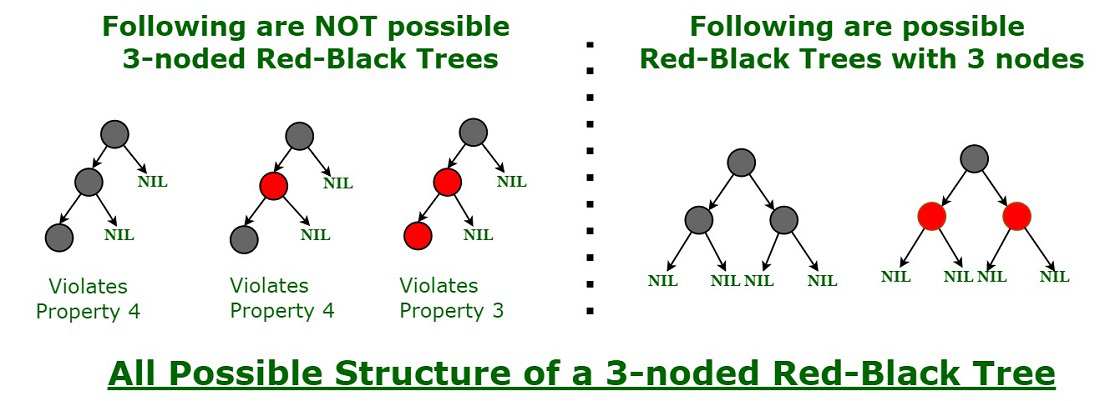
How does a Red-Black Tree ensure balance?

Applications:

• Most of the self-balancing BST library functions like map, multiset, and multimap in C++ ( or java packages like java.util.TreeMap and java.util.TreeSet ) use Red-Black Trees
• It is used to implement CPU Scheduling Linux
  • Completely Fair Scheduler uses it
• It is used in the K-mean clustering algorithm in machine learning for reducing time complexity
• MySQL also uses the Red-Black tree for indexes on tables in order to reduce the searching and insertion time

Insert and Delete

• search-tree operations TREE-INSERT and TREE-DELETE

  • when run on a red-black tree with n keys, take O(log n) time
    • Because they modify the tree, the result may violate the red-black properties
    • To restore these properties, we must change the colors of some nodes in the tree and also change the pointer structure

• We change the pointer structure through rotation

  • which is a local operation in a search tree that preserves the binary-search-tree property
  • When we do a left rotation on a node x
    • we assume that its right child y is not null
    • x may be any node in the tree whose right child is not null
    • The left rotation "pivots" around the link from x to y
    • It makes y the new root of the subtree, with x as ys left child and ys left child as xs right child

• rotate left example

  

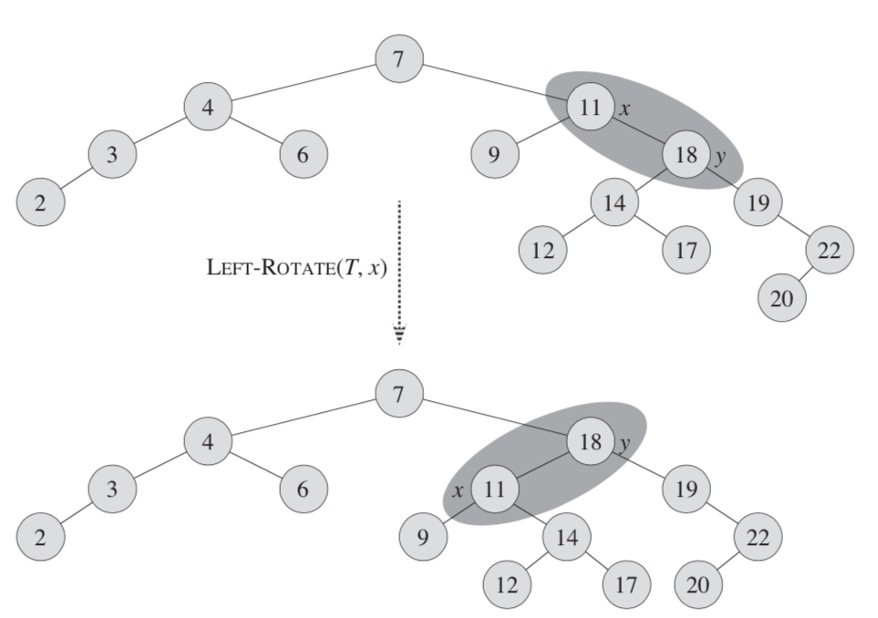
  • rotating element x in a tree T left
    • After a rotation, the y element "pulls" its right subtree up (elements 19, 20, 22)
    • Left subtree of x (9) stays the same, and left subtree of y becomes right subtree of x

  rotateLeft() {
    let y = this.right;
    this.right = y.left;
  
    if (!y.left.isNil) {
      y.left.parent = this;
    }
  
    if (!y.isNil) y.parent = this.parent;
  
    if (this.parent) {
      if (this.id === this.parent.left.id) {
        this.parent.left = y;
      } else {
        this.parent.right = y;
      }
    } else {
      this.tree.root = y;
    }
  
    y.left = this;
    if (!this.isNil) this.parent = y;
  }

• rotate right example

  rotateRight() {
    let y = this.left;
    this.left = y.right;
  
    if (!y.right.isNil) {
      y.right.parent = this;
    }
  
    if (!y.isNil) y.parent = this.parent;
  
    if (this.parent) {
      if (this.id === this.parent.right.id) {
        this.parent.right = y;
      } else {
        this.parent.left = y;
      }
    } else {
      this.tree.root = y;
    }
  
    y.right = this;
    if (!this.isNil) this.parent = y;
  }

Insertion

• To insert a node, first we have to find a place to insert it into

  • The new node will always be added as a leaf
  • This means that both of his children are NIL and are black
  • The newly added node will always be red

• example

  insertNode(data) {
    let current, parent, x;
    current = this.root;
    parent = null;
  
    while (!current.isNil) {
      if (data === current.value) return current;
  
      parent = current;
      current = data < current.value ? current.left : current.right;
    }
  
    x = new rbNode(this);
    x.value = data;
    x.parent = parent;
    x.isRed = true;
    x.isNil = false;
  
    x.left = new rbNode(this);
    x.right = new rbNode(this);
  
    if (parent) {
      if (x.value < parent.value) {
        parent.left = x;
      } else {
        parent.right = x;
      }
    } else {
      this.root = x;
    }
  
    this.insertFixup(x);
  
    return x;
  }

Insert Fix up

• After insertion, we perform a insertFixup operation defined as following

• example

  • To perform the fixup, we have to look at the parent, and check if the red-black property is followed
  • If the parent node is black
    • we can exit
  • If parent node is red
    • we recolor it black and preform a rotation to balance the tree
  • By inserting a red node with 2 NIL-children, we are keeping the property of black height (property 4)
    • Although, this could mean that we are breaking the property 3
      • according to which both children of a red node have to be black So, let's look at a situation when a parent of a new node is red, by which the property 3 will be violated

  insertFixup(x) {
    while (x.id !== this.root.id && x.parent.isRed) {
      if (x.parent.id === x.parent.parent.left.id) {
        let y = x.parent.parent.right;
  
        if (y.isRed) {
          x.parent.isRed = false;
          y.isRed = false;
          x.parent.parent.isRed = true;
          x = x.parent.parent;
        } else {
          if (x.id === x.parent.right.id) {
            x = x.parent;
            x.rotateLeft();
          }
  
          x.parent.isRed = false;
          x.parent.parent.isRed = true;
          x.parent.parent.rotateRight();
        }
      } else {
        let y = x.parent.parent.left;
  
        if (y.isRed) {
          x.parent.isRed = false;
          y.isRed = false;
          x.parent.parent.isRed = true;
          x = x.parent.parent;
        } else {
          if (x.id === x.parent.left.id) {
            x = x.parent;
            x.rotateRight();
          }
  
          x.parent.isRed = false;
          x.parent.parent.isRed = true;
          x.parent.parent.rotateLeft();
        }
      }
    }
  
    this.root.isRed = false;
  }