Binary Search: Advanced
Ugly Number III
Write a program to find the n-th ugly number.
Ugly numbers are positive numbers that are divisible by either a, b, or c.
Since the number can be too large, return the actual answer modulo 10^9 + 7
Example 1:
Input:n = 10, a = 2, b = 3, c = 5
Output: 14
Explanation: 2, 3, 4, 5, 6, 8, 9, 10, 12, 14 is the sequence of the first 10 ugly numbers.
Example 2:
Input:n = 2, a = 3, b = 4, c = 5
Output: 4
Explanation: 3, 4 is the sequence of the first 2 ugly numbers.
Constraints
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
function nthUglyNumber(n, a, b, c) {
const ab = leastCommonMultiple(a, b);
const bc = leastCommonMultiple(b, c);
const ac = leastCommonMultiple(a, c);
const abc = leastCommonMultiple(a, bc);
let low = Math.min(a, b, c);
let high = low * n;
while (low < high) {
const mid = ~~((high + low) / 2);
if (hasNthUglyNumbers(a, b, c, ab, bc, ac, abc, n, mid)) low = mid + 1;
else high = mid;
}
return low;
}
const greatestCommonDivisor = (a, b) => (b == 0 ? a : greatestCommonDivisor(b, a % b));
const leastCommonMultiple = (a, b) => (a * b) / greatestCommonDivisor(a, b);
const hasNthUglyNumbers = (a, b, c, ab, bc, ac, abc, n, mid) =>
~~(mid / a) +
~~(mid / b) +
~~(mid / c) -
~~(mid / ab) -
~~(mid / bc) -
~~(mid / ac) +
~~(mid / abc) <
n;
Explanation
- For this question, we can go through linearly and determine the value of the next ugly number
- The time complexity is
O(n)- That is not enough, though, as n can reach
10^9Can we do better?
- That is not enough, though, as n can reach
- by using binary search
- The time complexity is
O(log(n))
- The time complexity is
Count in constant time
- Consider a given integer k,
- we can calculate the number of ugly numbers less than or equal to it by checking how many numbers are divisible by either a, b, or c
- We can find the number of numbers divisible by x by k / x
- e.g. there are two numbers less than or equal to 10 that are divisible by 5 - 5 and 10
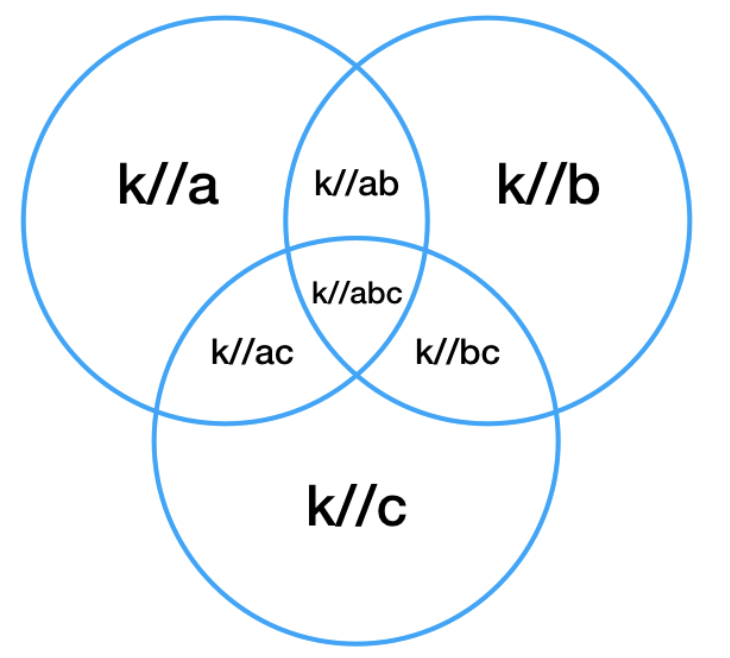
- To find the number of numbers divisible by three different numbers, we can use the following Venn Diagram
Total area = k//a + k//b + k//c - k//ab - k//bc - k//ac + k//abc
Monotonic condition
- Also note that the number of ugly numbers below k can never decrease as k increase
- so we can perform a binary search to find the least k such that there are at least n ugly numbers less than or equal to it