Sorting

• stable sorting algorithm means that when two elements have the same value, their relative order is maintained
  • e.g. if we are sorting a hand of cards, and we have a Seven of Hearts before a Seven of Spades in the initial hand
    • after a stable sort, the Seven of Hearts is still before the Seven of Spades because their values are the same
    • However, in an unstable algorithm, the Seven of Spades might appear before the Seven of Hearts
    • The above is only true when we are comparing the cards by value, not suit
    • That is, two cards of the same value can be different
• in-place sorting algorithm means that the algorithm does not use additional data structure to hold temporary data
  • Additional memory cannot be avoided (as swapping two elements involve additional memory)
    • but they should be something like a temporary variable that uses very little additional memory

Algorithm	Best Time	Average Time	Worst Time	Space
Bubble Sort	Ω(n^2)	θ(n^2)	O(n^2)	O(1)
Selection Sort	Ω(n^2)	θ(n^2)	O(n^2)	O(1)
Revised Bubble Sort	Ω(n)	θ(n^2)	O(n^2)	O(1)
Insertion Sort	Ω(n)	θ(n^2)	O(n^2)	O(1)
Quick Sort	Ω(n log(n))	θ(n log(n))	O(n^2)	O(log(n))
Tree Sort	Ω(n log(n))	θ(n log(n))	O(n^2)	O(n)
Bucket Sort	Ω(n + k)	θ(n + k)	O(n^2)	O(n)
Heap Sort	Ω(n log(n))	θ(n log(n))	O(n log(n))	O(1)
Merge Sort	Ω(n log(n))	θ(n log(n))	O(n log(n))	O(n)
Shell Sort	Ω(n)	θ(n log(n))	O(n log(n))	O(1)
Cube Sort	Ω(n)	θ(n log(n))	O(n log(n))	O(n)
Tim Sort	Ω(n)	θ(n log(n))	O(n log(n))	O(n)
Radix Sort	Ω(nk)	θ(nk)	O(nk)	O(n + k)
Count Sort	Ω(n + k)	θ(n + k)	O(n + k)	O(k)

Insertion Sort

• idea of an insertion sort is initially, only the first item is considered sorted
  • Then, for each item in the sequence, we "insert" that item into the sorted list by swapping that item with the item before it
  • until the item before it is smaller than the current item
• Imagine you are sorting a hand of cards
  • What people usually do is maintain a pile of sorted cards
  • and inserting from the unsorted pile into the sorted pile in the correct position
• It is a stable algorithm because later elements will not swap with earlier elements unless the later element is smaller
• it is an in-place algorithm because no additional data structure is used to store intermediate values
• good for sorting lists that are almost sorted
  • number of swaps required to insert an item when the list is almost sorted is close to O(1)

JavaScript

function sortList(unsortedList) {
  for (let i = 0; i < unsortedList.length; i++) {
    let current = i;
    while (current > 0 && unsortedList[current] < unsortedList[current - 1]) {
      [unsortedList[current], unsortedList[current - 1]] = [
        unsortedList[current - 1],
        unsortedList[current],
      ];
      current--;
    }
  }
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(test);

input: [5, 3, 1, 2, 4]

current = 0, move to next loop

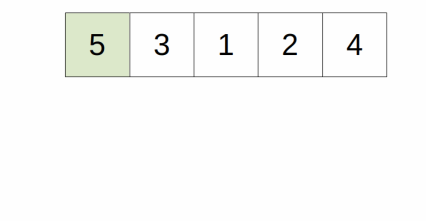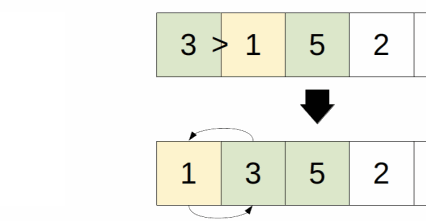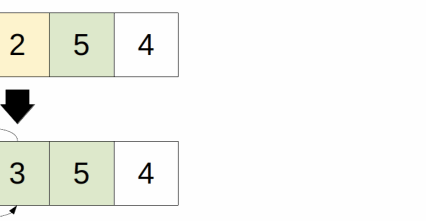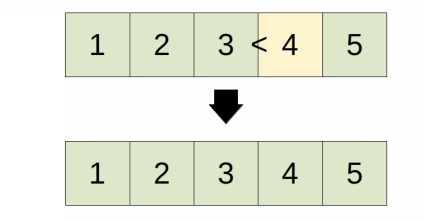
current = 1, is input[1] < input[0] = true
3 < 5, swap 3 with 5 = [3, 5, 1, 2, 4]
current = 0, move to next loop

current = 2, is input[2] < input[1] = true
1 < 5, swap 1 with 5 = [3, 1, 5, 2, 4]
current = 1, is input[1] < input[0] = true
1 < 3, swap 1 with 3 = [1, 3, 5, 2, 4]
current = 0, move to next loop

current = 3, is input[3] < input[2] = true
2 < 5, swap 2 with 5 = [1, 3, 2, 5, 4]
current = 2, is input[2] < input[1] = true
2 < 3, swap 2 with 3 = [1, 2, 3, 5, 4]
current = 1, is input[1] < input[0] = false
2 > 1, no swap = [1, 2, 3, 5, 4]
current = 0, move to next loop

current = 4, is input[4] < input[3] = true
4 < 5, swap 4 with 5 = [1, 2, 3, 4, 5]
current = 3, is input[3] < input[2] = false
4 > 3, no swap = [1, 2, 3, 4, 5]
current = 2, is input[2] < input[1] = false
3 > 2, no swap = [1, 2, 3, 4, 5]
current = 1, is input[1] < input[0] = false
3 > 1, no swap = [1, 2, 3, 4, 5]
current = 0, end loop

output: [1, 2, 3, 4, 5]

time space complexity

• For each n item in the list, the time complexity to insert it into the sorted list is O(i)
  • where i is the index of that item
• Overall, the time complexity is O(n * (n - 1) / 2)
  • which is equivalent to O(n^2)

Selection Sort

• during each cycle, we find the smallest item from the unsorted pile and add it to the sorted pile
• To find the smallest element in the unsorted pile
  • have a temporary variable keeping track of the index to the smallest element
  • compare each element in the unsorted pile to that element, updating the new index if necessary
• After all the elements have been compared
  • swap the smallest index with the first index of the unsorted pile
  • The element is now part of the sorted pile
• not a stable algorithm because an earlier element can jump after an element of the same value during a swap
• algorithm is in-place as it only needs additional memory to store the index to the minimum element
• even if the list is almost sorted, we still need to go through the entire process each cycle

JavaScript

function sortList(unsortedList) {
  const n = unsortedList.length;
  for (let i = 0; i < n; i++) {
    let minIndex = i;
    for (let j = i; j < n; j++) {
      if (unsortedList[j] < unsortedList[minIndex]) {
        minIndex = j;
      }
    }
    [unsortedList[i], unsortedList[minIndex]] = [
      unsortedList[minIndex],
      unsortedList[i],
    ];
  }
  return unsortedList;
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(test);

input: [5, 3, 1, 2, 4]

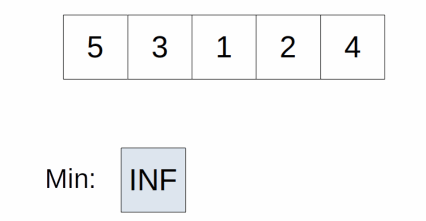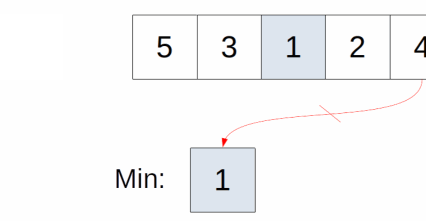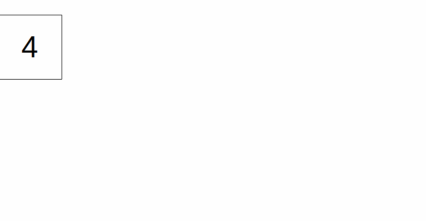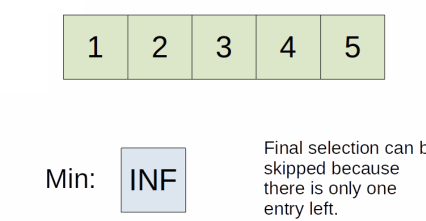
minIndex = 0, is input[0] < input[0] = false
5 === 5, no change in minIndex, move to next loop
minIndex = 0, is input[1] < input[0] = true
3 < 5, change minIndex to 1, move to next loop
minIndex = 1, is input[2] < input[1] = true
1 < 3, change minIndex to 2, move to next loop
minIndex = 2, is input[3] < input[2] = false
2 > 1, no change in minIndex, move to next loop
minIndex = 2, is input[4] < input[2] = false
4 > 1, no change in minIndex, end loop
swap input[0] with input[2] = swap 5 with 1 = [1, 3, 5, 2, 4]
move to next loop

minIndex = 1, is input[1] < input[1] = false
3 === 3, no change in minIndex, move to next loop
minIndex = 1, is input[2] < input[1] = false
5 > 3, no change in minIndex, move to next loop
minIndex = 1, is input[3] < input[1] = true
2 < 3, change minIndex to 3, move to next loop
minIndex = 3, is input[4] < input[3] = false
4 > 2, no change in minIndex, end loop
swap input[1] with input[3] = swap 3 with 2 = [1, 2, 5, 3, 4]
move to next loop

minIndex = 2, is input[2] < input[2] = false
5 === 5, no change in minIndex, move to next loop
minIndex = 2, is input[3] < input[2] = true
3 < 5, change minIndex to 3, move to next loop
minIndex = 3, is input[4] < input[3] = false
4 > 3, no change in minIndex, end loop
swap input[2] with input[3] = swap 5 with 3 = [1, 2, 3, 5, 4]
move to next loop

minIndex = 3, is input[3] < input[3] = false
5 === 5, no change in minIndex, move to next loop
minIndex = 3, is input[4] < input[3] = true
4 < 5, change minIndex to 4, end loop
swap input[3] with input[4] = swap 5 with 4 = [1, 2, 3, 4, 5]

minIndex = 4, is input[4] < input[4] = false
5 === 5, no change in minIndex, end loop
end loop

output: [1, 2, 3, 4, 5]

time space complexity

• For each n item in the list, the time complexity to find the smallest item in the unsorted pile is O(n - i)
  • where i is the index of that item
• Overall, the time complexity is O(n * (n + 1) / 2)
  • which is equivalent to O(n^2)

Bubble Sort

• idea of bubble sort is for each pass, we use a pointer to point at the first element of the list
  • For each cycle, we compare it to the next element in the list
  • and swap them if the current item is greater
  • then move the pointer by one until it reaches the end of the list
  • We repeat this process until the list becomes sorted
  • The list is sorted if, during a pass, no swapping occurs
• Note that during each pass, the largest element will always "float" to the top, like a bubble
  • Therefore, each pass, we only need to consider the interval excluding the last element of the previous interval
    • and the list is guaranteed to be sorted within n passes
• It is a stable algorithm because a swap cannot cause an element to move past another one with the same value
  • and it is in-place because no additional data structure is used
• good for sorting lists that are almost sorted
  • after close to O(1) bubbles we can detect that the list is already sorted and stop the sorting

JavaScript

function sortList(unsortedList) {
  const n = unsortedList.length;
  for (let i = n - 1; i >= 0; i--) {
    let swapped = false;
    for (let j = 0; j < i; j++) {
      if (unsortedList[j] > unsortedList[j + 1]) {
        [unsortedList[j], unsortedList[j + 1]] = [
          unsortedList[j + 1],
          unsortedList[j],
        ];
        swapped = true;
      }
    }
    if (!swapped) return unsortedList;
  }
  return unsortedList;
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(test);

input: [5, 3, 1, 2, 4]

i=4
set swapped to false
loop 4 times
1st loop is input[j] > input[j+1] = true
5 > 3, swap 5 with 3 = [3, 5, 1, 2, 4], set swapped to true
2nd loop is input[j] > input[j+1] = true
5 > 1, swap 5 with 1 = [3, 1, 5, 2, 4], set swapped to true
3rd loop is input[j] > input[j+1] = true
5 > 2, swap 5 with 2 = [3, 1, 2, 5, 4], set swapped to true
4th loop is input[j] > input[j+1] = true
5 > 4, swap 5 with 4 = [3, 1, 2, 4, 5], set swapped to true, end inner loop
since swapped is true, move to next outer loop

i=3
set swapped to false
loop 3 times
1st loop is input[j] > input[j+1] = true
3 > 1, swap 3 with 1 = [1, 3, 2, 4, 5], set swapped to true
2nd loop is input[j] > input[j+1] = true
3 > 2, swap 3 with 2 = [1, 2, 3, 4, 5], set swapped to true
3rd loop is input[j] > input[j+1] = false
3 < 4, swap 3 with 2 = [1, 2, 3, 4, 5], end inner loop
since swapped is true, move to next outer loop

i=2
set swapped to false
loop 2 times
1st loop is input[j] > input[j+1] = false
1 < 2, no swap, move to next inner loop
2nd loop is input[j] > input[j+1] = false
2 < 3, no swap, end inner loop
since swapped is false, end outer loop and return sorted array

output: [1, 2, 3, 4, 5]

time space complexity

• time complexity of this algorithm is O(n^2)
  • because it is essentially two loops

Merge Sort

• idea of a merge sort is divide and conquer
  • We divide the array into two almost equally
    • sort them (usually another merge sort)
    • and merge the two sorted list into one
  • To merge the two sorted list
    • have two pointers point towards the bottom of the two list
    • and each step, add the smaller element from those two into the list
    • and move the pointer of that item up by one until elements from both lists are fully added
• Assume the sorting of the divided list is stable, the overall algorithm is stable
  • because if an element appears before another element with the same value, there are two situations
    1. If they are in the same list
       • the first element is before the second one in that list
       • and the first one will be inserted first
    2. If they are in different lists
       • the first element will be inserted first if two elements are equal
• Note that the base case, where only one element exists in the list is stable
  • because there are no 2 elements of the same size, so merge sort is stable
• merge sort is not in-place because of the usage of additional arrays
• merge sort is stable, and always have a time complexity of O(nlog(n))
  • so it is more reliable compared to quick sort
• requires way more extra memory than quick sort, and requires memory management of arrays, so quick sort is often preferred if stability is not important
• it is a classic Divide and Conquer algorithm
  • has applications in real-world interview questions such as Count of Smaller Numbers after Self

JavaScript

Recursion

function merge(leftList, rightList, midIndex, n) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;
  while (leftIndex < midIndex || rightIndex < n - midIndex) {
    if (leftIndex === midIndex) {
      result.push(rightList[rightIndex]);
      rightIndex++;
    } else if (rightIndex === n - midIndex) {
      result.push(leftList[leftIndex]);
      leftIndex++;
    } else if (leftList[leftIndex] <= rightList[rightIndex]) {
      result.push(leftList[leftIndex]);
      leftIndex++;
    } else {
      result.push(rightList[rightIndex]);
      rightIndex++;
    }
  }
  return result;
}

function sortList(unsortedList) {
  const n = unsortedList.length;
  if (n <= 1) return unsortedList;

  const midIndex = Math.floor(n / 2);
  const leftList = sortList(unsortedList.slice(0, midIndex));
  const rightList = sortList(unsortedList.slice(midIndex));
  const sortedList = merge(leftList, rightList, midIndex, n);
  return sortedList;
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(result);

input: [5, 3, 1, 2, 4]

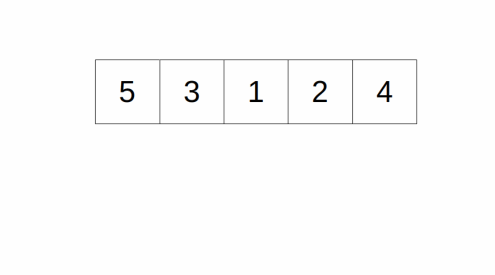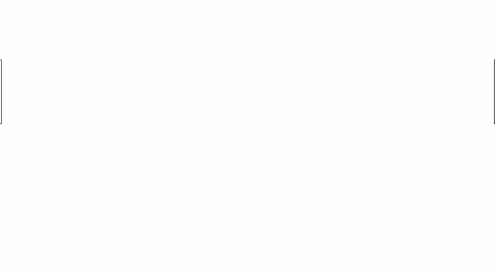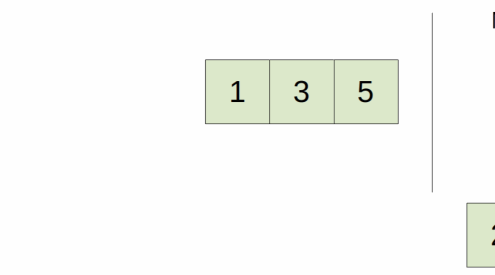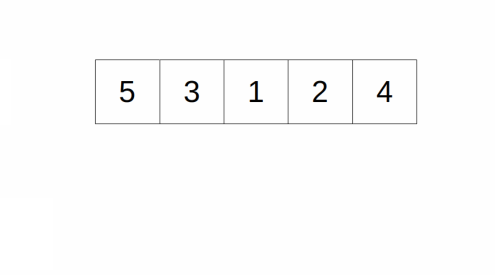
  [5, 3, 1, 2, 4]
   /         \
[5, 3]    [1, 2, 4]
n > 1, midIndex is 2
work on the original left half first [5, 3]
add sortList(unsortedList.slice(0, 2)) to the stack
------------------
|sortList([5, 3])|
------------------

new unsortedList is [5, 3]
 [5, 3]
 /   \
[5]  [3]
since n > 1, new midIndex is 1
work on the new 1st left half [5]
new unsortedList is [5]
since n = 1, return [5]
------------------
|sortList([5, 3])|
------------------

leftList = [5]
work on the new 1st right half [3]
new unsortedList = [3]
since n = 1, return [3]
------------------
|sortList([5, 3])|
------------------

rightList = [3]
start merging leftList = [5] and rightList = [3]
midIndex remains at 1, n remains at 2
leftIndex = 0, rightIndex = 0, loop starts
since leftList[leftIndex] > rightList[rightIndex], 5 > 3
3 is added to the result array, rightIndex increment by 1 and is now 1, go to next loop
result array is [3]
since rightIndex === n - midIndex, 1 === 2 - 1
5 is added to the result array, leftIndex increment by 1 and is now 1
both leftIndex === midIndex & rightIndex === n - midIndex, end loop
result array is [3, 5]
--------
|[3, 5]|
--------
original left array = [3, 5]

new unsortedList is [1, 2, 4]
work on the original right half first [1, 2, 4]
add sortList(unsortedList.slice(2)) to the stack
---------------------
|sortList([1, 2, 4])|
---------------------

 [1, 2, 4]
  /     \
[1]    [2, 4]
new unsortedList is [1]
work on the new 2nd left half [1]
since n = 1, return [1]

leftList = [1]
work on the new 2nd right half [2, 4]
add sortList(unsortedList.slice(1)) to the stack
---------------------
|sortList([2, 4])   |
|sortList([1, 2, 4])|
---------------------

new unsortedList is [2, 4]
 [2, 4]
 /   \
[2]  [4]
since n > 1, new midIndex is 1
work on the new 3rd left half [2]
new unsortedList is [2]
since n = 1, return [2]

leftList = [2]
work on the new 3rd right half [4]
new unsortedList is [4]
since n = 1, return [4]

rightList = [4]
start merging leftList = [2] and rightList = [4]
midIndex is 1, n is 2
leftIndex = 0, rightIndex = 0, loop starts
since leftList[leftIndex] < rightList[rightIndex], 2 < 4
2 is added to the result array, leftIndex increment by 1 and is now 1, go to next loop
result array is [2]
since rightIndex === n - midIndex, 1 === 2 - 1
4 is added to the result array, leftIndex increment by 1 and is now 1
both leftIndex === midIndex & rightIndex === n - midIndex, end loop
result array is [2, 4]
return [2, 4]
---------------------
|[2, 4]             |
|sortList([1, 2, 4])|
---------------------

start merging leftList = [1] and rightList = [2, 4]
midIndex is 1, n is 3
leftIndex = 0, rightIndex = 0, loop starts
since leftList[leftIndex] < rightList[rightIndex], 2 < 4
1 is added to the result array, leftIndex increment by 1 and is now 1, go to next loop
since leftIndex === midIndex at 1
2 is added to the result array, rightIndex increment by 1 and is now 1, go to next loop
since leftIndex === midIndex at 1
4 is added to the result array, rightIndex increment by 1 and is now 1, go to next loop
both leftIndex === midIndex & rightIndex === n - midIndex, end loop
result array is [1, 2, 4]
return [1, 2, 4]
------------------
|[1, 2, 4]       |
------------------

  [5, 3, 1, 2, 4]
   /         \
[3, 5]    [1, 2, 4]
original right array is [1, 2, 4]
start merging leftList = [3, 5] and rightList = [1, 2, 4]
midIndex is 2, n is 5
leftIndex = 0, rightIndex = 0, loop starts
since leftList[leftIndex] > rightList[rightIndex], 3 > 1
1 is added to the result array, rightIndex increment by 1 and is now 1, go to next loop
since leftList[leftIndex] > rightList[rightIndex], 3 > 2
2 is added to the result array, rightIndex increment by 1 and is now 2, go to next loop
since leftList[leftIndex] < rightList[rightIndex], 3 < 4
3 is added to the result array, leftIndex increment by 1 and is now 2, go to next loop
since leftList[leftIndex] > rightList[rightIndex], 5 > 4
4 is added to the result array, rightIndex increment by 1 and is now 3, go to next loop
since rightIndex === n - midIndex, 3
5 is added to the result array, left Index increment by 1 and is now 3, go to next loop
both leftIndex === midIndex & rightIndex === n - midIndex, end loop
result array is [1, 2, 3, 4, 5]
return [1, 2, 3, 4, 5]

output: [1, 2, 3, 4, 5]

Iterative

• also known as bottom up merge sort
  • we treat each element of the array as n sub arrays
  • then iteratively merge these sub array back and forth between two buffers

function merge(left, right, leftLimit, rightLimit, sorted, buffer) {
  let i = left;

  //Compare the two sub arrays and merge them in the sorted order
  while (left < leftLimit && right < rightLimit) {
    if (sorted[left] <= sorted[right]) {
      buffer[i++] = sorted[left++];
    } else {
      buffer[i++] = sorted[right++];
    }
  }

  //If there are elements in the left sub arrray then add it to the result
  while (left < leftLimit) {
    buffer[i++] = sorted[left++];
  }

  //If there are elements in the right sub array then add it to the result
  while (right < rightLimit) {
    buffer[i++] = sorted[right++];
  }
}

function sortList(unsortedList) {
  //Create two arrays for sorting
  let sorted = [...unsortedList];
  let n = sorted.length;
  let buffer = new Array(n);

  for (let size = 1; size < n; size *= 2) {
    for (let leftStart = 0; leftStart < n; leftStart += 2 * size) {
      //Get the two sub arrays
      let left = leftStart;
      let right = Math.min(left + size, n);
      let leftLimit = right;
      let rightLimit = Math.min(right + size, n);

      //Merge the sub arrays
      merge(left, right, leftLimit, rightLimit, sorted, buffer);
    }

    //Swap the sorted sub array and merge them
    [sorted, buffer] = [buffer, sorted];
  }

  return sorted;
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(result);

input: [5, 3, 1, 2, 4]

create a new input array copy sorted = [5, 3, 1, 2, 4] and a new array buffer = [, , , , ] for sorting
n = 5
start outer loop, 1st loop, size = 1, 1 < n
start inner loop, 1st loop, leftStart = 0, 0 < n
get the 2 sub arrays
left = 0, since left + size < n, 0 + 1 < 5, right = 1
leftLimit = 1, since right + size < n, 1 + 1 < 5, rightLimit = 2
merge sub arrays [5], [3]

i = left = 0
is left < leftLimit and right < rightLimit, 0 < 1 and 1 < 2, true
start compare 2 sub arrays and merge them loop
is sorted[left] > sorted[right], 5 > 3, true
set buffer[i] = sorted[right], buffer[0] = sorted[1] = 3, increment i and right by 1, i = 1, right = 2
buffer [3, , , , ]
since right === rightLimit, loop breaks

check if elements in left sub array exist then add to buffer
is left < leftLimit, 0 < 1, true
buffer[i] = sorted[left], buffer[1] = sorted[1], buffer[1] = 5, increment i and left by 1, i = 2, left = 1
buffer [3, 5, , , ]
since left === leftLimit, 1 === 1, loop breaks

check if elements in right sub array exists then add to buffer
is right < rightLimit, 2 === 2, false, loop does not start


2nd inner loop, leftStart = 0 + 2 * 1 = 2, 2 < n
get the 2 sub arrays
left = 2, since left + size < n, 2 + 1 < 5, right = 3
leftLimit = 3, since right + size < n, 3 + 1 < 5, rightLimit = 4
merge sub arrays [1], [2]

i = left = 2
is left < leftLimit and right < rightLimit, 2 < 3 and 3 < 4, true
start compare 2 sub arrays and merge them loop
is sorted[left] < sorted[right], 1 < 2, true
set buffer[i] = sorted[left], buffer[2] = sorted[2] = 1, increment i and left by 1, i = 3, left = 3
buffer [3, 5, 1, , ]
since left === leftLimit, loop breaks

check if elements in left sub array exists then add to buffer
is left < leftLimit, 3 === 3, false, loop does not start

check if elements in right sub array exist then add to buffer
is right < rightLimit, 3 < 4, true
buffer[i] = sorted[right], buffer[3] = sorted[3], buffer[3] = 2, increment i and right by 1, i = 4, right = 4
buffer [3, 5, 1, 2, ]
since right === rightLimit, 4 === 4, loop breaks


3rd inner loop, leftStart = 2 + 2 * 1 = 4, 4 < n
get the 2 sub arrays
left = 4, since left + size === n, 4 + 1 === 5, right = 5
leftLimit = 5, since right + size > n, 5 + 1 > 5, rightLimit = 5
merge sub arrays [4], []

i = left = 4
is left < leftLimit and right < rightLimit, 4 < 5 and 5 < 5, false, loop does not start

check if elements in left sub array exist then add to buffer
is left < leftLimit, 4 < 5, true
buffer[i] = sorted[left], buffer[4] = sorted[4], buffer[4] = 4, increment i and left by 1, i = 5, left = 5
buffer [3, 5, 1, 2, 4]
since left === leftLimit, 5 === 5, loop breaks

check if elements in right sub array exists then add to buffer
is right < rightLimit, 5 === 5, false, loop does not start


since leftStart = 4 + 2 * 1 = 6, 6 > n, inner loop breaks
swap buffer with sorted array
new sorted array = [3, 5, 1, 2, 4], new buffer array values [5, 3, 1, 2, 4] are not important


2nd outer loop, size = 1 * 2 = 2, 2 < n
start inner loop, 1st loop, leftStart = 0, 0 < n
get the 2 sub arrays
left = 0
right = 2, since left + size < n, 0 + 2 < 5
leftLimit = 2
rightLimit = 4, since right + size < n, 2 + 2 = 4 < 5
merge sub arrays [3, 5], [1, 2]

i = left = 0
is left < leftLimit and right < rightLimit, 0 < 2 and 2 < 4, true
start compare 2 sub arrays and merge them loop
is sorted[left] > sorted[right], 3 > 1, true
set buffer[i] = sorted[right], buffer[0] = sorted[2] = 1, increment i and right by 1, i = 1, right = 3
buffer [1, 3, 1, 2, 4]
since right < rightLimit, loop continues
is sorted[left] > sorted[right], 3 > 2, true
set buffer[i] = sorted[right], buffer[1] = sorted[3] = 2, increment i and right by 1, i = 2, right = 4
buffer [1, 2, 1, 2, 4]
since right === rightLimit, loop breaks

check if elements in left sub array exist then add to buffer
is left < leftLimit, 0 < 2, true
buffer[i] = sorted[left], buffer[2] = sorted[0], buffer[2] = 3, increment i and left by 1, i = 3, left = 1
buffer [1, 2, 3, 2, 4]
since left < leftLimit, 1 < 2, loop continues
is left < leftLimit, 1 < 2, true
buffer[i] = sorted[left], buffer[3] = sorted[1], buffer[3] = 5, increment i and left by 1, i = 4, left = 2
buffer [1, 2, 3, 5, 4]
since left === leftLimit, loop breaks

check if elements in right sub array exists then add to buffer
is right < rightLimit, 4 === 4, false, loop does not start


2nd inner loop, leftStart = 0 + 2 * 2, 4 < n
get the 2 sub arrays
left = 4
right = 5, since left + size < n, 4 + 2 = 6 > 5
leftLimit = 5
rightLimit = 5, since right + size < n, 5 + 2 = 7 > 5
merge sub arrays [4], []

i = left = 4
is left < leftLimit and right < rightLimit, 4 < 5 and 5 < 5, false, loop does not start

check if elements in left sub array exist then add to buffer
is left < leftLimit, 4 < 5, true
buffer[i] = sorted[left], buffer[4] = sorted[4], buffer[4] = 4, increment i and left by 1, i = 5, left = 5
buffer [1, 2, 3, 5, 4]
since left === leftLimit, 5 === 5, loop breaks

check if elements in right sub array exists then add to buffer
is right < rightLimit, 5 === 5, false, loop does not start


since leftStart = 4 + 2 * 2 = 8, 8 > n, inner loop breaks
swap buffer with sorted array
new sorted array = [1, 2, 3, 5, 4], new buffer array values [3, 5, 1, 2, 4] are not important


3rd outer loop, size = 2 * 2 = 4, 4 < n
start inner loop, 1st loop, leftStart = 0, 0 < n
get the 2 sub arrays
left = 0
right = 4, since left + size < n, 0 + 4 < 5
leftLimit = 4
rightLimit = 5, since right + size < n, 4 + 4 = 8 > 5
merge sub arrays [1, 2, 3, 5], [4]

i = left = 0
is left < leftLimit and right < rightLimit, 0 < 4 and 4 < 5, true
start compare 2 sub arrays and merge them loop
is sorted[left] < sorted[right], 1 < 4, true
set buffer[i] = sorted[left], buffer[0] = sorted[0] = 1, increment i and left by 1, i = 1, left = 1
buffer [1, 5, 1, 2, 4]
since left < leftLimit, loop continues
is sorted[left] < sorted[right], 2 < 4, true
set buffer[i] = sorted[left], buffer[1] = sorted[1] = 2, increment i and left by 1, i = 2, left = 2
buffer [1, 2, 1, 2, 4]
since left < leftLimit, loop continues
is sorted[left] < sorted[right], 3 < 4, true
set buffer[i] = sorted[left], buffer[2] = sorted[2] = 3, increment i and left by 1, i = 3, left = 3
buffer [1, 2, 3, 2, 4]
since left < leftLimit, loop continues
is sorted[left] > sorted[right], 5 < 4, true
set buffer[i] = sorted[right], buffer[3] = sorted[4] = 4, increment i and right by 1, i = 4, right = 5
buffer [1, 2, 3, 4, 4]
since right === rightLimit, 5 === 5, loop breaks

check if elements in left sub array exist then add to buffer
is left < leftLimit, 3 < 4, true
buffer[i] = sorted[left], buffer[4] = sorted[3], buffer[4] = 5, increment i and left by 1, i = 5, left = 4
buffer [1, 2, 3, 4, 5]
since left === leftLimit, 4 === 4, loop breaks

check if elements in right sub array exists then add to buffer
is right < rightLimit, 5 === 5, false, loop does not start


since leftStart = 4 + 2 * 2 = 8, 8 > n, inner loop breaks
swap buffer with sorted array
new sorted array = [1, 2, 3, 4, 5], new buffer array values [1, 2, 3, 5, 4] are not important

3rd outer loop, size = 4 * 2 = 8, 8 > n, outer loop breaks

output: [1, 2, 3, 4, 5]

time space complexity

• overall time complexity is O(nlog(n))
  • because for each item in the list
    • it is merged a number of times equal to the number of divisions to make to divide the list to a size of one
      • which is O(log(n)) times

Quick Sort

• idea of quick sort is We select an arbitrary element in the list (known as the "pivot")
  • we swap the elements in the list into two sides
    • a side where all the elements are smaller than the pivot
    • a side where all the elements are larger or equal to the pivot
  • After grouping them this way, we swap the pivot with the first element of the side that is larger or equal to the pivot
  • This way, each element to the left of the pivot is smaller than the pivot
    • and each element on the right is larger or equal to pivot
  • Then we just need to sort the left interval and the right interval (using the same method), then the list would be sorted
• how would it grouped together?
  • for the interval that we are sorting, we have a pointer point before the start and at the end (including the pivot)
  • For each swap, we move the start pointer until we find an element >= to the pivot (after the initial index)
    • and move the end pointer until we find an element <= to the pivot (before the initial index)
  • Then we can swap those two elements and restart the process
  • If those two pointers meet, we stop and then we can swap the pivot and the meeting point
• algorithm is not stable, as each swap skips a lot of values
• It sort the array in-place, as it does not require additional data structures
  • Note that this does not mean this algorithm happens in constant space
• merge sort is stable, and always have a time complexity of O(nlog(n))
  • so it is more reliable compared to quick sort
• requires way more extra memory than quick sort, and requires memory management of arrays, so quick sort is often preferred if stability is not important
• A problem with the following implementation of quick sort is that when the list is almost sorted, it will take close to O(n^2) time
  • In other implementations, however, the pivot is selected as the midpoint of the list, so it can help mitigate this problem
    • however, you would need to remember that the index to the pivot moves with the pivot when swapping
• unlikely you will be asked to code it up at an interview
  • but the idea of moving things around a pivot can be seen in Two Pointers interview questions

JavaScript

function sortListInterval(unsortedList, start, end) {
  if (end - start <= 1) return undefined;
  const pivot = unsortedList[end - 1];
  let startPointer = start;
  let endPointer = end - 1;
  while (startPointer < endPointer) {
    while (unsortedList[startPointer] < pivot && startPointer < endPointer) {
      startPointer++;
    }
    while (unsortedList[endPointer] >= pivot && startPointer < endPointer) {
      endPointer--;
    }
    if (startPointer === endPointer) {
      break;
    }
    [unsortedList[startPointer], unsortedList[endPointer]] = [
      unsortedList[endPointer],
      unsortedList[startPointer],
    ];
  }
  [unsortedList[startPointer], unsortedList[end - 1]] = [
    unsortedList[end - 1],
    unsortedList[startPointer],
  ];
  sortListInterval(unsortedList, start, startPointer);
  sortListInterval(unsortedList, startPointer + 1, end);
}

function sortList(unsortedList) {
  sortListInterval(unsortedList, 0, unsortedList.length);
  return unsortedList;
}

const test = [5, 3, 1, 2, 4];
const result = sortList(test);
console.log(test);

input: [5, 3, 1, 2, 4]

n = 5
set start as 0, end as 5
end - start = 5 - 0 = 5 <= 1, false, continue
pivot = array[end - 1] = array[4] = 4
startPointer = start = 0
endPointer = end - 1 = 5 - 1 = 4
is startPointer < endPointer, 0 < 4, true, start 1st outer loop
is array[startPointer] < pivot && startPointer < endPointer, array[0] < 4 && 0 < 4, 5 < 4 && 0 < 4, false, loop does not start
is array[endPointer] >= pivot && startPointer < endPointer, array[4] >= 4 && 0 < 4, 4 >= 4 && 0 < 4, true, start 1st inner loop
endPointer decrement by 1, endPointer = 3
array[3] >= 4 && 0 < 3, 2 >= 4 && 0 < 3, false, end inner loop
is startPointer === endPointer, 0 === 3, false, continue
swap array[startPointer] with array[endPointer], array[0] with array[3], 5 with 2
[5, 3, 1, 2, 4] -> [2, 3, 1, 5, 4]

is startPointer < endPointer, 0 < 3, true, continue 2nd outer loop
is array[startPointer] < pivot && startPointer < endPointer, array[0] < 4 && 0 < 3, 2 < 4 && 0 < 3, true, start 1st inner loop
startPointer increment by 1, startPointer = 1
array[1] < 4 && 1 < 3, 3 < 4 && 1 < 3, true, continue 2nd inner loop
startPointer increment by 1, startPointer = 2
array[2] < 4 && 2 < 3, 1 < 4 && 2 < 3, true, continue 2nd inner loop
startPointer increment by 1, startPointer = 3
array[3] < 4 && 3 < 3, 5 < 4 && 3 < 3, false, break inner loop

is array[endPointer] >= pivot && startPointer < endPointer, array[3] >= 4 && 3 < 3, 5 >= 4 && 3 < 3, false, loop does not start
is startPointer === endPointer, 3 === 3, true, break outer loop
swap array[startPointer] with array[end - 1], array[3] with array[4], 5 with 4
[2, 3, 1, 5, 4] -> [2, 3, 1, 4, 5]

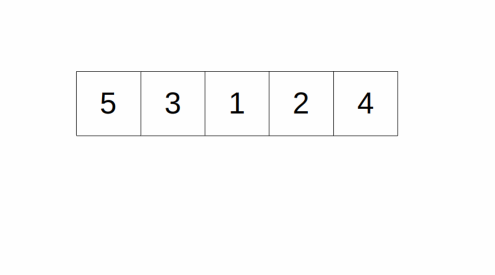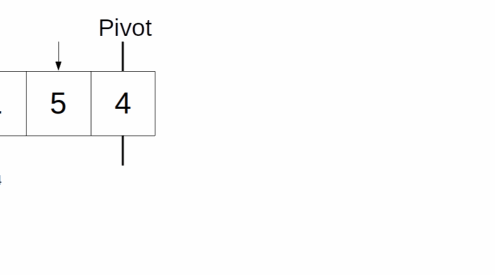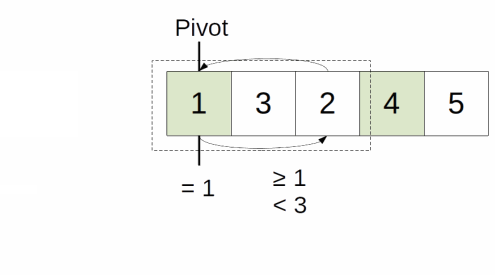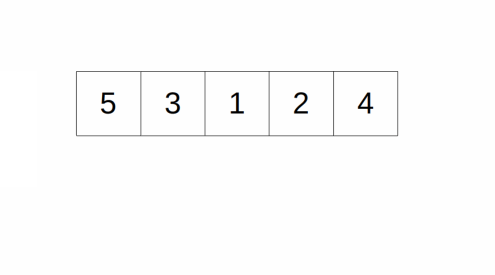
call 1st left recursion
start = 0
end = startPointer = 3
end - start = 3 - 0 = 3 <= 1, false, continue
pivot = array[end - 1] = array[3 - 1] = array[2] = 1
startPointer = start = 0
endPointer = end - 1 = 3 - 1 = 2
is startPointer < endPointer, 0 < 2, true, start 1st outer loop
is array[startPointer] < pivot && startPointer < endPointer, array[0] < 1 && 0 < 2, 2 < 1 && 0 < 2, false, loop does not start
is array[endPointer] >= pivot && startPointer < endPointer, array[2] >= 1 && 0 < 2, 1 >= 1 && 0 < 2, true, start 1st inner loop
endPointer decrement by 1, endPointer = 1
array[1] >= 1 && 0 < 1, 3 >= 1 && 0 < 1, true, continue 2nd inner loop
endPointer decrement by 1, endPointer = 0
array[0] >= 1 && 0 < 0, 2 >= 1 && 0 < 0, false, end inner loop
is startPointer === endPointer, 0 === 0, end outer loop
swap array[startPointer] with array[end - 1], array[0] with array[2], 2 with 1
[2, 3, 1, 4, 5] -> [1, 3, 2, 4, 5]

call 2nd left recursion
start = 0
end = startPointer = 0
end - start = 0 - 0 = 0 <= 1, true, return undefined

call 2nd right recursion
start = startPointer + 1 = 0 + 1 = 1
end = 3
end - start = 3 - 1 = 2 <= 1, false, continue
pivot = array[end - 1] = array[3 - 1] = array[2] = 2
startPointer = start = 1
endPointer = end - 1 = 3 - 1 = 2
is startPointer < endPointer, 1 < 2, true, start 1st outer loop
is array[startPointer] < pivot && startPointer < endPointer, array[1] < 2 && 1 < 2, 3 < 2 && 1 < 2, false, loop does not start
is array[endPointer] >= pivot && startPointer < endPointer, array[2] >= 2 && 1 < 2, 2 >= 2 && 1 < 2, true, start 1st inner loop
endPointer decrement by 1, endPointer = 1
array[1] >= 2 && 1 < 1, 3 >= 2 && 1 < 1, false, end inner loop
is startPointer === endPointer, 1 === 1, end outer loop
swap array[startPointer] with array[end - 1], array[1] with array[2], 3 with 2
[1, 3, 2, 4, 5] -> [1, 2, 3, 4, 5]

call 3rd left recursion
start = 1
end = startPointer = 1
end - start = 1 - 1 = 0 <= 1, true, return undefined

call 3rd right recursion
start = startPointer + 1 = 1 + 1 = 2
end = 3
end - start = 3 - 2 = 1 <= 1, true, return undefined

call 1st right recursion
start = startPointer + 1 = 3 + 1 = 4
end = 5
end - start = 5 - 4 = 1 <= 1, true, return undefined

output: [1, 2, 3, 4, 5]

time space complexity

• The time complexity of quick sort is a bit complicated
• On average, where the list is divided somewhere near the center each time, the time complexity is O(nlog(n))
• However, in the worst case scenario, each interval to sort is one less than the current interval
  • which would make the time complexity O(n^2)
    • This depends heavily on which pivot point you chooses
      • if you choose an end point as your pivot and the list is already sorted, it will reach this time complexity
      • Otherwise, the chance of this happening is very low
• uses recursion as its core logic, and the minimum recursion layers is equal to log(n)

Heap sort

• utilizes a heap and pull the elements from the heap and order them
• is unstable, and can be done in-place

time space complexity

• It has a time complexity of O(nlog(n))

Tree sort

• utilizes a binary search tree that is built from the list, so we can iterate through it
• can be stable, but is not in-place

time space complexity

• It has a time complexity of O(nlog(n)) (if balanced)

Bucket sort

• can use if there are a lot of integers to be sorted, but the range of these integers are very small
• uses an array, with the index being the entries from the list and the value being the number of times a number has appeared in the list

time space complexity

• has a worst time complexity of O(n^2)
• has a space complexity of O(m), where m is the range of the integers

Built-in sorting

• most modern programming language have a built-in sorting function
• in an interview, it is sufficient to just use these built-in ones

Python

unsorted = [5, 3, 1, 2, 4]

result = sorted(unsorted)
print(unsorted)  # [5, 3, 1, 2, 4]
print(result)  # [1, 2, 3, 4, 5]

unsorted1 = [5, 3, 1, 2, 4]
unsorted1.sort()
print(unsorted1)  # [1, 2, 3, 4, 5]

Javascript

const unsorted = [5, 3, 1, 2, 4];

const result = unsorted.sort();
console.log(unsorted); // [1, 2, 3, 4, 5]
console.log(result); // [1, 2, 3, 4, 5]