Backtracking: Dedup
Subsets
Given a set of distinct integers, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example 1:
Input: nums = [1,2,3]
Output:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
- Solution 1: permutations
function subsets(nums) {
const result = [];
dfs(0, [], nums, result);
return result;
}
function dfs(i, current, nums, result) {
const n = nums.length;
if (i === n) {
result.push(current);
return;
}
dfs(i + 1, current.concat([nums[i]]), nums, result);
dfs(i + 1, current, nums, result);
}
- Solution 2: combination sum
function subsets(nums) {
const result = [[]];
dfs(0, [], nums, result);
return result;
}
function dfs(i, current, nums, result) {
const n = nums.length;
if (i === n) return;
const newCurrent = current.concat([nums[i]]);
result.push(newCurrent);
dfs(i + 1, newCurrent, nums, result);
dfs(i + 1, current, nums, result);
}
- Solution 3: iterative
function subsets(nums) {
let result = [[]];
backtrack(0, [], nums, result);
return result;
}
function backtrack(first, current, nums, result) {
// we iterate over the indexes i from 'first' to the length
//of the entire sequence 'nums'
for (let i = first; i < nums.length; i++) {
current.push(nums[i]);
// use distructure operator to clone 'current' value and save to 'result'
result.push([...current]);
// generate all other subsets for the current subset.
// increasing the position by one to avoid duplicates in 'result'
backtrack(i + 1, current, nums, result);
// BACKTRACK.
current.pop();
}
}
Explanation
- Time Complexity:
O(2^n) - We have to permute through the possibilities
State-space tree
- Similar to permutations, we make a binary choice of whether to include the number in the subset at each level
- We can use a state i to keep track of the index of the current char we are at
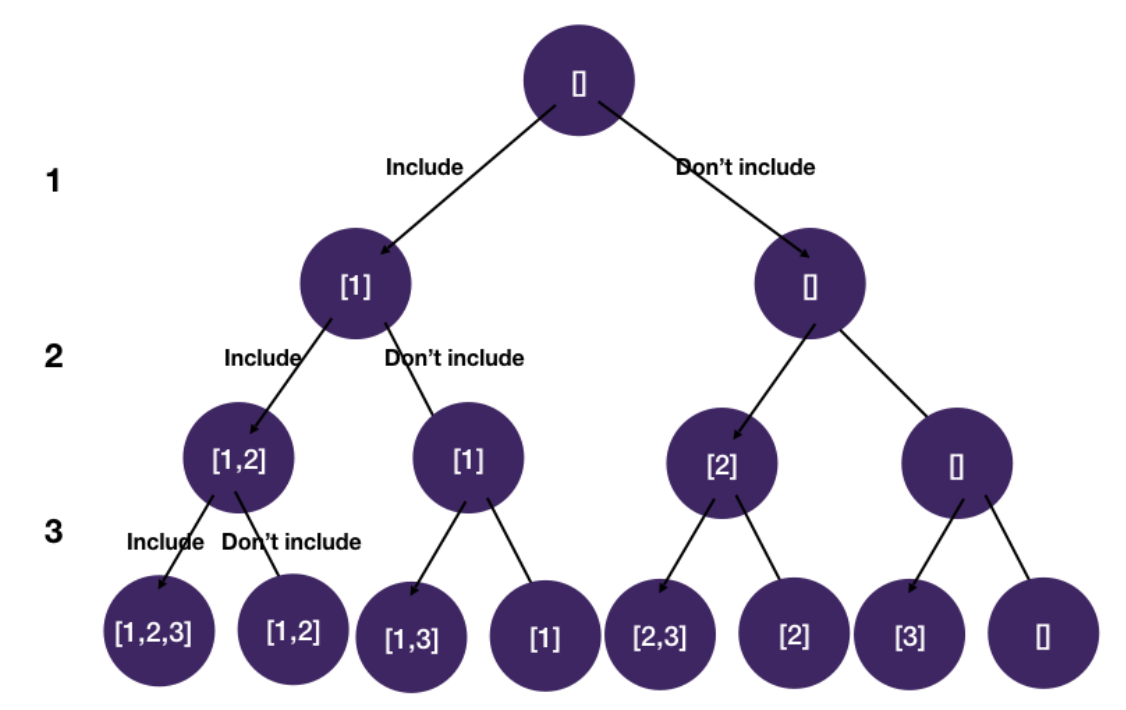
Alternative solution
- Note that this problem is very special because every time we make a choice we already have a subset
- so some of the leaf node values are in internal nodes as well
- Therefore, we can potentially terminate the search earlier
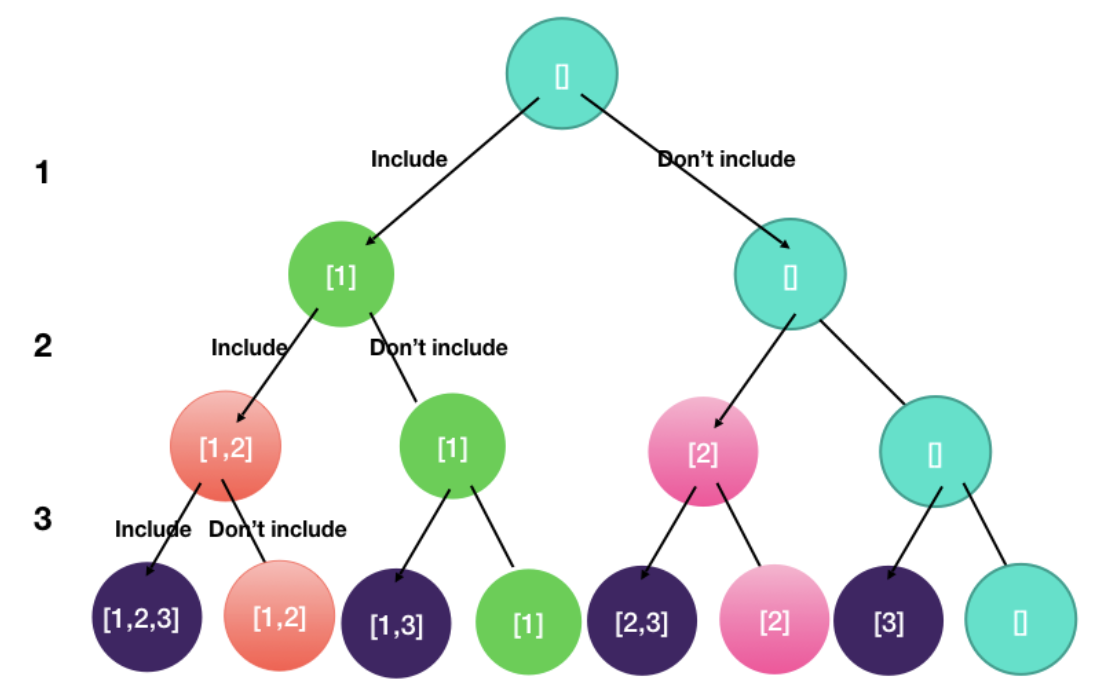
- An alternative and faster solution to is take advantage of the fact that internal nodes are also final states and draw the tree differently
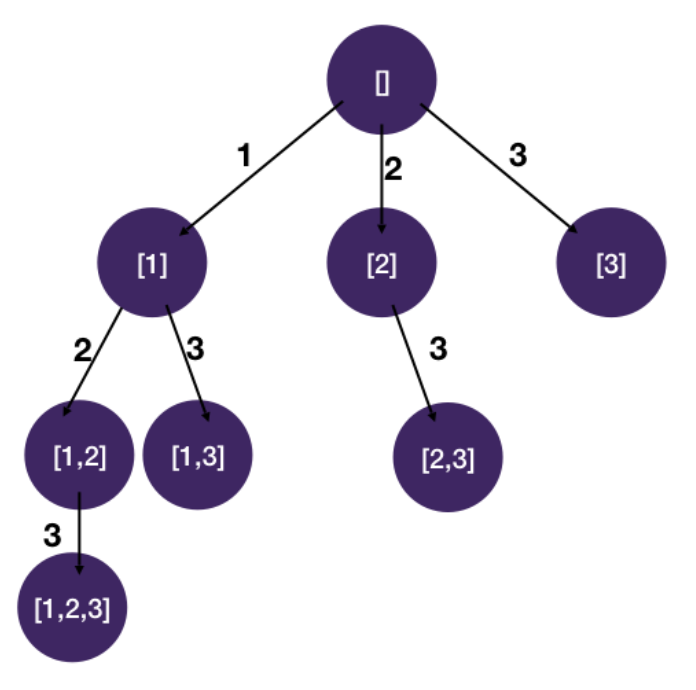
- Similar to combination sum, we dedup by only pruning backward branches
- Note that the main difference between the alternate solution and the original is the position of the res.append(cur)
- We don't wait until we get to a leaf node to add to the result list
- We instead add to the result list at each step