Linear Algebra

It is the study of vectors and linear functions.

• Explanation 1:
  • It is a branch of mathematics that lets you concisely describe coordinates and interactions of planes in higher dimensions and perform operations on them.
• Explanation 2:
  • Linear algebra is a branch of mathematics that deals with vectors (quantities with both magnitude and direction), matrices (rectangular arrays of numbers), and linear transformations (functions that preserve addition and scalar multiplication).
• Explain like I am 5
  • Imagine you have a bunch of LEGO blocks. Each block is like a number, and you can stack them differently. If you line them up in rows and columns, that’s like a matrix. If you push or stretch them in a certain direction, that’s like a transformation. Linear algebra helps us understand how things change when we add, move, or pull these blocks in a straight and predictable way. It’s like playing with numbers in an organized way.
• it is 1 of the main building blocks of machine learning

Applications in Machine Learning

1. Data set and Date Files
   • We fit the model on a data set in ML
   • This data set is either a matrix or a vector
   • e.g.: our model could be a fitness-related model that predicts the quality of sleep
2. Images and Photographs
   • Computer vision application
     • you cannot send an image to a model and expect it to understand
     • each image is made of pixels that are colored squares of varying intensities
     • a black and white image is a single-pixel
     • a colored image has 3-pixel values for RGB
     • all images are stored as a matrix
     • each operation (e.g.: cropping, scaling, et cetera) that is performed on the image is described using the notation and operations of linear algebra
3. Data Preparation
   • dimensionality reduction
     • usually, we come across data that is made up of thousands of variables and our model becomes extremely complicated
     • this is when dimensionality reduction comes into play
     • data sets are represented as matrices and then we can use matrix factorization methods to reduce it into its constituent parts
   • 1 hot encoding
     • it is used when working with categorical data
       • such as class labels for classification problems or categorical input variables
     • it is common to encode categorical variables to make them easier to work with
4. Linear Regression
   • Used for predicting numerical values in simple regression problems
   • the most common way of solving linear regression is via the least squares optimization which is solved using matrix factorization methods from linear regression
5. Regularization
   • Overfitting is 1 of the greatest obstacles in ML
   • When a model is too close a fit for the available data to the point that it does not perform well with any new or outside data
   • It is a concept from Linear algebra that is used to prevent the model from overfitting
   • Simple models are models that have smaller coefficient values
   • It is a technique that is often used to encourage a model to minimize the size of coefficients while it's being fit on data
6. Principal Component Analysis (PCA)
   • modeling data with many features is challenging and it's hard to know which features of data are relevant and which are not
   • 1 of the methods for automatically reducing the number of columns of a data set is principle component analysis
   • this method is used in ML to create projections of high dimensional data for both visualization and training models
   • The core of the PCA method is a metric factorization method
7. Latent Semantic Analysis (LSA)
   • it is a form of data preparation used in natural language processing, a subfield of ML for working with text data
   • in this case, documents are usually represented as a large matrix of word occurrences
   • then we can apply matrix factorization methods to them to be able to easily compare, query, and use them as the basis for the ML model
8. Recommender Systems
   • They are used each time you buy something on Amazon or a similar shop and you get recommendations of products based on your previous purchases
9. Deep Learning (DL)
   • it is a specific subfield of ML
   • Scaled up to multiple dimensions, DL methods work with vectors, matrices, and tensors of inputs and coefficients

Vectors

Scalar

• it is just a number
• we denote a scalar with a lower-case symbol, such as a or b
• e.g.: weight, temperature, blood pressure
  • they are represented by numbers such as 200 pounds, 55 Fahrenheit, or 120 by 80

Vector

• The 2 most important characteristics of vectors

1. Dimensionality
   • the number of elements in a vector
   • it is called length or the shape of the vector in python
2. Orientation
   • whether the vector is in column orientation standing up tall, or row orientation laying flat and wide

• Vector Examples

• Orientation usually doesn't matter, but when performing arithmetic operations it is extremely important
  • wrong orientation leads to unexpected results or even errors

• If they're row-oriented, then they are written as with t where t indicates the transpose operation which converts a column vector into a row vector.

• the red arrow v is the vector

• a and b are scalars denoting the magnitude of v in horizontal and vertical directions.

• The algebraic interpretation of a vector is an ordered list of numbers.

• The geometric interpretation of a vector is a line that has a specific length and direction also called an angle.

• It is computed relative to the positive X-axis.

• The two points of a vector are called the tail, where the vector starts, and the head which has the arrow tip, where it ends.

• Vector Representation in python

# Many linear algebra operations don't work on Python lists, we create vectors as NumPy arrays called ND (N-dimensional) arrays
vectorAsList = [1, 2, 3, 4, 5]

# This array is an orientation-less array meaning it's neither a row nor a column vector
vectorAsArray = np.array([1, 2, 3, 4, 5])

# In NumPy, we indicate orientation with brackets
# the outer brackets just group all elements together in one object as an additional set of brackets indicates a row
rowVector = np.array([[1, 2, 3, 4, 5]])

# It has only one column and five rows
columnVector = np.array([[1], [2], [3], [4], [5]])

Vector addition

• To add two vectors, add each corresponding element.
• We cannot add a three-dimensional vector with a four-dimensional vector
• dimensions don't match the error example

import numpy as np

a = np.array([20, 40, 60])
b = np.array(10, 20, 30)
c = np.array([5, 10, 15, 20])

a + b  # array([30, 60, 90])

a + c  # ValueError: operands could not be broadcast together with shapes (3,) (4,)

• To add two vectors, you have to place the vectors such that the tail of one vector is at the head of the other vector.
• The sum vector traverses from the tail of the first vector to the head of the second

Vector Subtraction

• We cannot subtract a three-dimensional vector from a four-dimensional vector
• dimensions don't match the error example

import numpy as np

a = np.array([20, 40, 60])
b = np.array(10, 20, 30)
c = np.array([5, 10, 15, 20])

a - b  # array([10, 20, 30])

a - c  # ValueError: operands could not be broadcast together with shapes (3,) (4,)

• To subtract vectors, you have to up the two vectors such that their tails are at the same coordinate.
• The difference vector is the line that goes from the head of the negative vector to the head of the positive vector.

Vector Multiplication

• example

import numpy as np

a = np.array([20, 40, 60])
b = np.array(10, 20, 30)
c = np.array([5, 10, 15, 20])

a * b  # array([200, 800, 1000])

Vector Division

import numpy as np

a = np.array([20, 40, 60])
b = np.array(10, 20, 30)
c = np.array([5, 10, 15, 20])

a / b  # array([2., 2., 2.])

Vector Scalar multiplication

• multiply each vector element by the scalar
• example

import numpy as np

scalar = 2

list_a = [10, 11, 12, 13, 14, 15]

list_as_array = np.array(list_a)  # [10 11 12 13 14 15]

scalar * list_a  # This is wrong, value is [10, 11, 12, 13, 14, 15, 10, 11, 12, 13, 14, 15]

scalar * list_as_array  # array([20, 22, 24, 26, 28, 30])

• we have four possible cases that depend on whether the scalar is
  • greater than 1
  • between 1 and 0
  • exactly 0
  • or negative
    • Only in the case when the scalar is negative, the direction of the vector will change

Cartesian Coordinate System

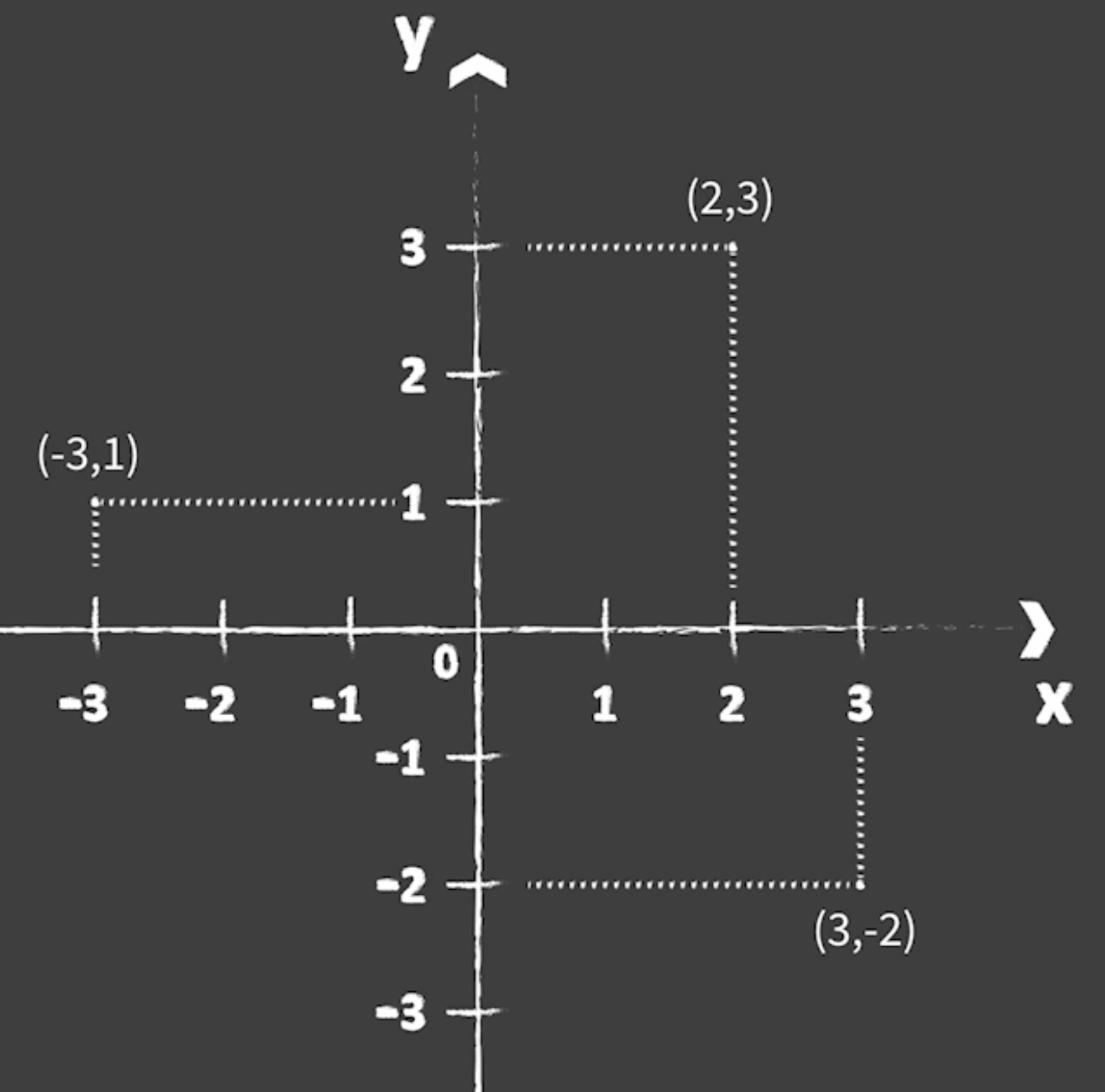
• we can locate a point by its combination of numbers
• it is important because it describes where a certain position is located in a 2-dimensional area
• Coordinates have 2 numbers (x-coordinate and y-coordinate)
• The x-axis runs left and right, the y-axis runs up and down
• The axes x and y meet at (0, 0) coordinate at the center which is called the origin
• A point is denoted by its distance along the x-axis followed by its distance along the y-axis

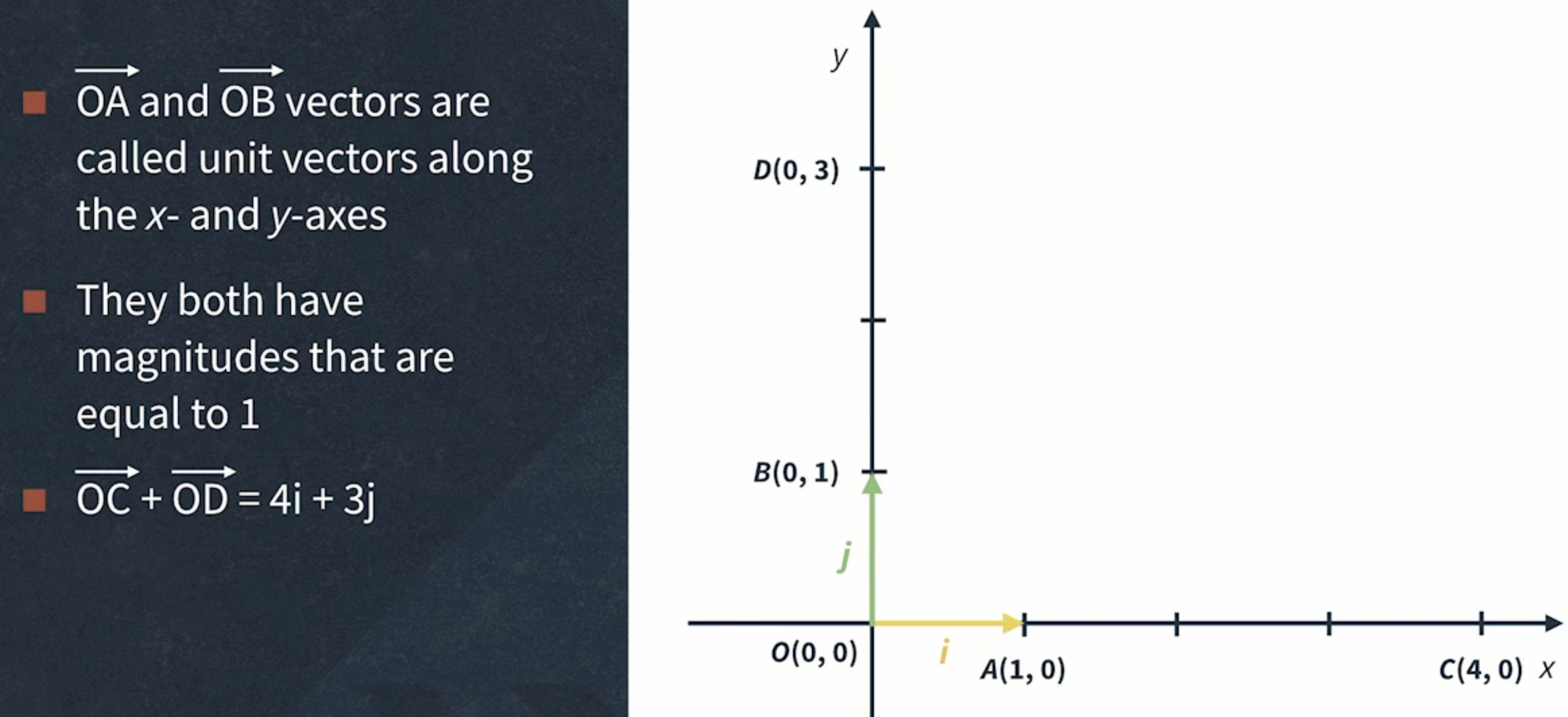
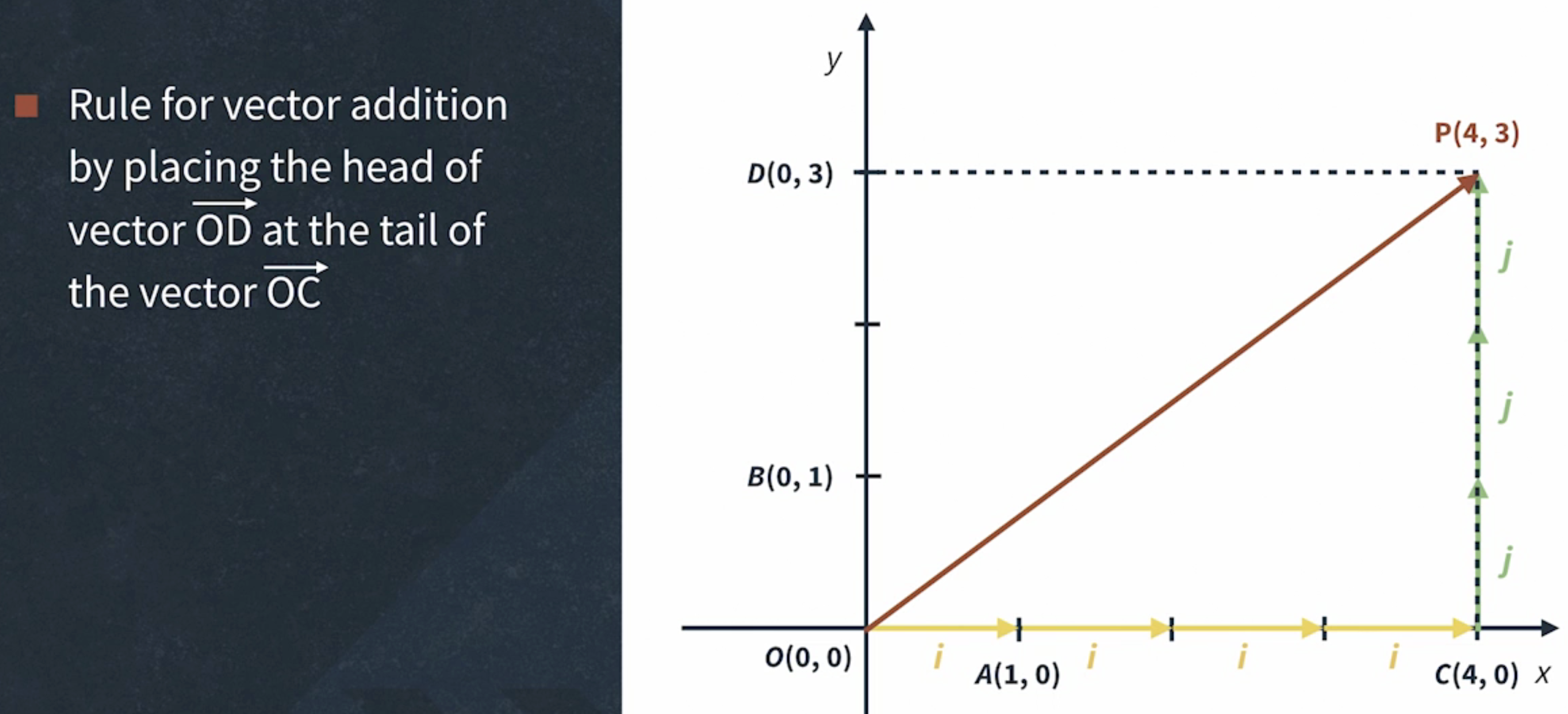
Vector Projections and Basis

Dot Product of Vectors

• it is widely used in ML, in many operations and algorithms

• 3 different ways it can be represented with symbols

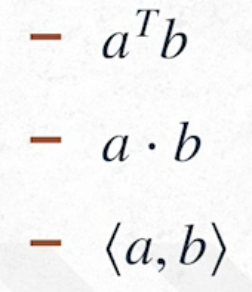
• Dot notation

  • the dot product of 2 vectors is calculated by multiplying their corresponding elements by each other and then summing them all
  • it is a single number that provides information about the relationship between 2 vectors
  • It could be represented with the following formula, where a and b are vectors of the same dimensionality and ai represents the ith element of a

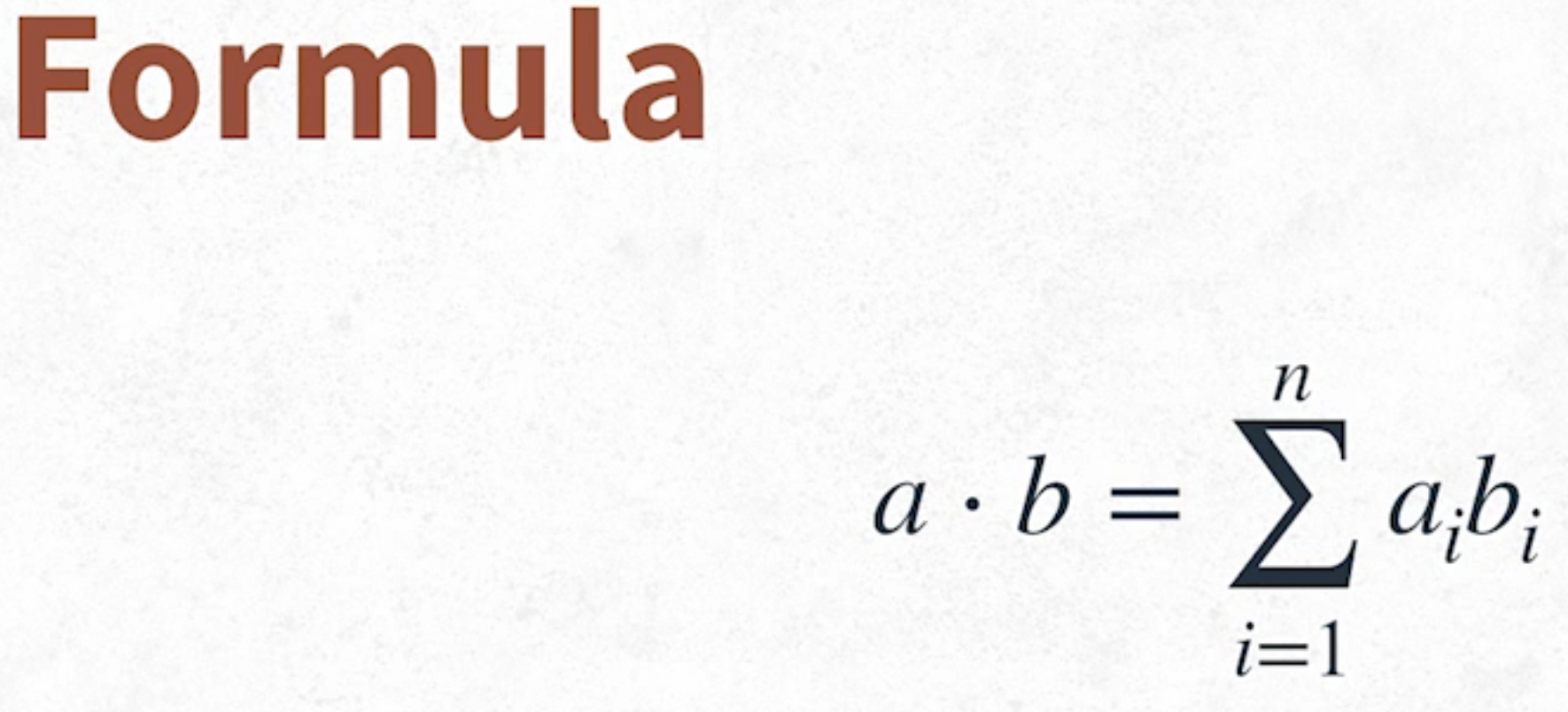
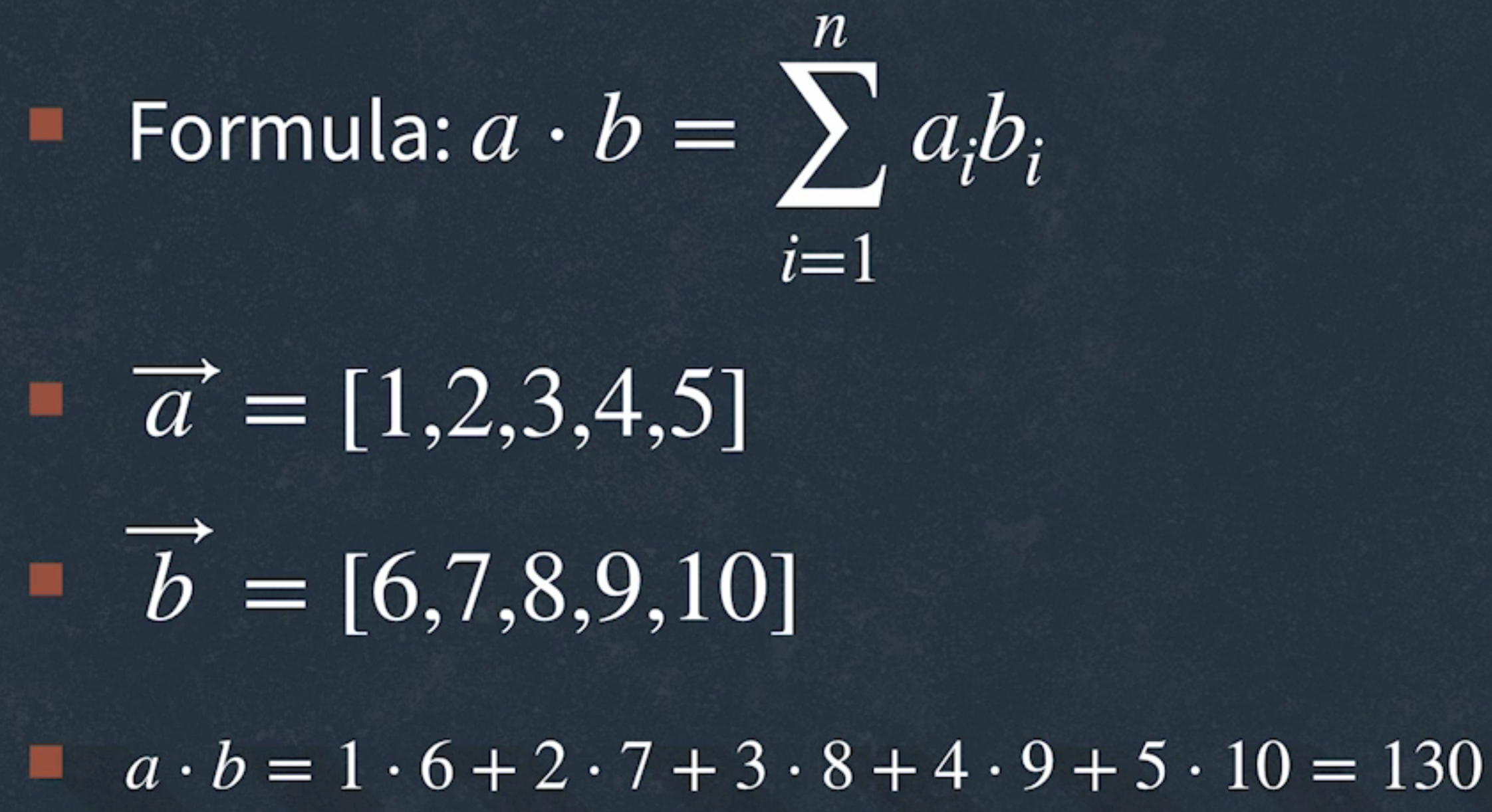
import numpy as np

a = np.array([1, 2, 3, 4, 5])
b = np.array([6, 7, 8, 9, 10])

np.dot(a, b)  # 130

• Basic Properties of Dot Product
  • The dot product is a commutative operation, meaning if vectors switch places, the dot product stays the same
    • a . b = b . a
  • the dot product is distributive over addition, meaning the following formula applies
    • a(b + c) = a . b + a . c

import numpy as np

a = np.array([1, 2, 3, 4, 5])
b = np.array([6, 7, 8, 9, 10])

np.dot(a, b)  # 130

c = np.array([11, 12, 13, 14, 15])

np.dot(b, a)  # 130

first_result = np.dot(a, b + c)  # 335

second_result = np.dot(a, b) + np.dot(a, c)  # 335

Scalar and Vector Projection

• it is an important part of ML because it makes mathematical operations and applying ML models easier
• Magnitude of a Vector
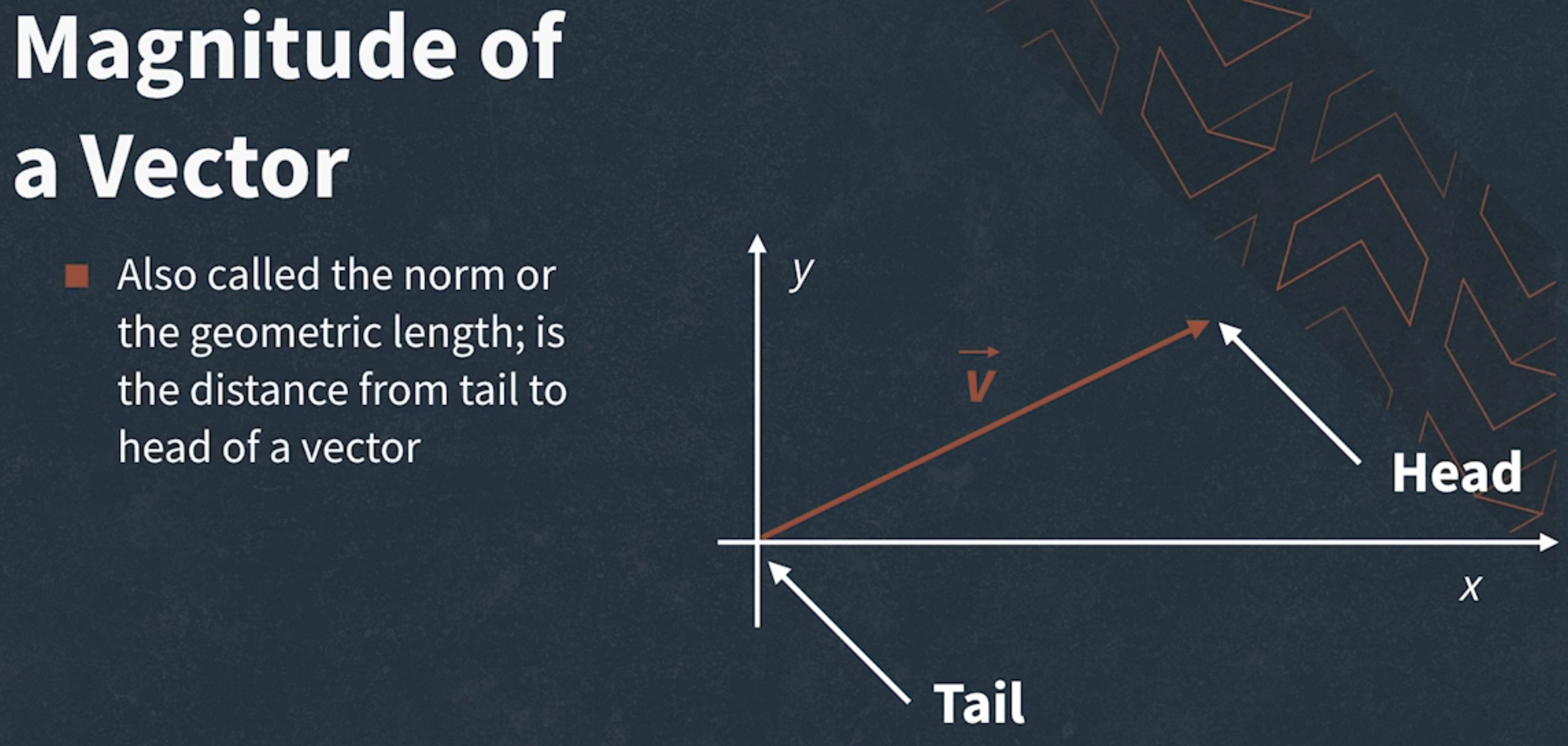
  • it computes using the standard Euclidean distance formula
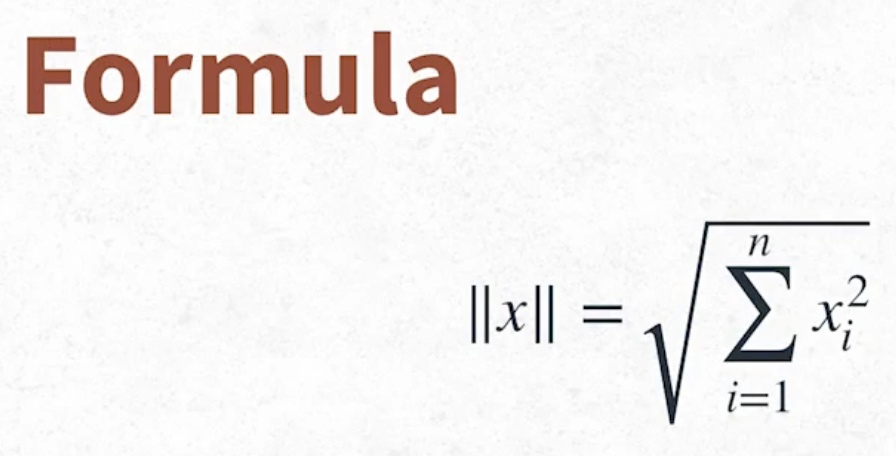
    • Vector magnitude is indicated using double vertical bars around the vector ||x||

import numpy as np

x = np.array([1,2,3,4,5])

np.linalg.norm(x)  # np.float64(7.416198487095663)