Two Pointer: Cycle Finding

Linked List Cycle

Given a linked list with potentially a loop,
determine whether the linked list from the first node contains a cycle in it.
For bonus points, do this with constant space.

Parameters
  nodes: The first node of a linked list with potentially a loop.
Result
  Whether there is a loop contained in the linked list.

Example 1
Input:
  0 -> 1 -> 2 -> 3 -> 4
       ^              |
       | - - - - - - - 
 
Output: true

Example 2
Input:
  0 -> 1 -> 2 -> 3 -> 4

Output: false

Constraints
  1 <= len(nodes) <= 10^5

class Node {
  constructor(val, next = null) {
    this.val = val;
    this.next = next;
  }
}

function hasCycle(head) {
  let fast = head;
  let slow = head;
  while (slow && fast) {
    fast = fast?.next?.next;
    slow = slow?.next;
    if (!fast || !slow) break;
    if (fast === slow) return true;
  }
  return false;
};

Explanation

• If a linked list has no loop, then when we iterate through the list, we will eventually reach the end of the list
  • at which point we can simply return
  • However, the challenge is figuring out how to terminate the program if it finds a loop
    • Otherwise the program would go on forever
• A simple solution would be to use a set to store the information
  • We store all the nodes we have been through and check if we have been there each time we move
  • However, a set is not constant memory, and there might be issues with hashing and whatnot
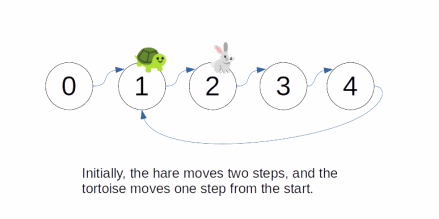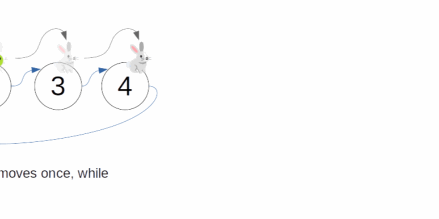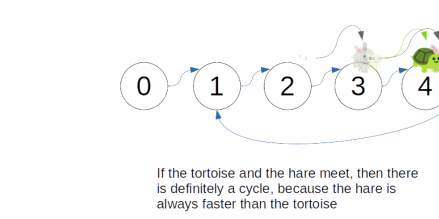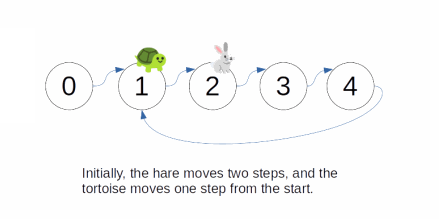
• Introducing Floyd's Cycle Finding Algorithm also known as the Tortoise and Hare Algorithm
  • The idea is to have two pointers, the fast pointer (or "hare") moves at double speed of the slow pointer (or "tortoise")
  • Each cycle, the tortoise moves once and the hare moves twice
  • The idea is that since the cycle must have integer size
    • when the tortoise and the hare are both in the cycle
    • their distance difference must also be an integer
  • Then, each cycle, because of their speed difference
    • the distance between them constantly reduces until they meet
    • in which case we know there is a cycle
  • However, if there is no cycle, they will never meet because the speed of the hare is always faster
• Time Complexity: O(n)
  • Technically O(n/2) but again we factor out the constant and we are left with linear time
  • Worst case we have, O(2n) as the small pointer moves around the entire array once
  • Either way we have O(n) time complexity