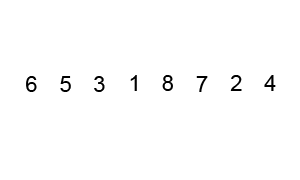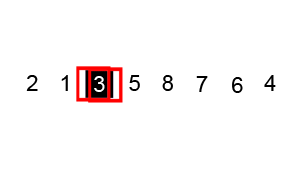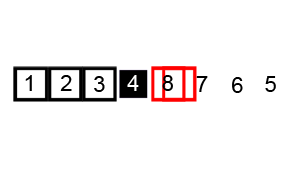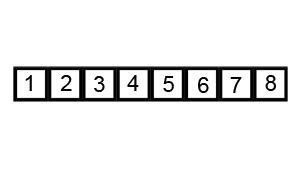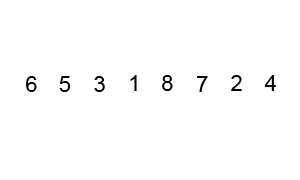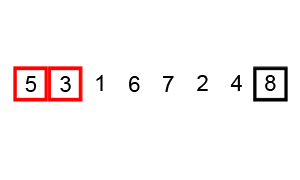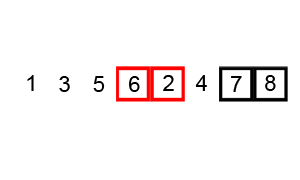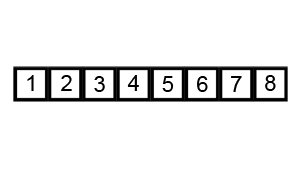Sorting algorithms

Algorithm	Time best case	Time avg case	Time worst case	Space
Quicksort	`O(n log n)`	`O(n log n)`	`O(n²)`	`O(log n)`
Bubble Sort	`O(n)`	`O(n²)`	`O(n²)`	`O(1)`
Counting Sort	`O(n + k)`	`O(n + k)`	`O(n + k)`	`O(n + k)`
Selection Sort	`O(n²)`	`O(n²)`	`O(n²)`	`O(1)`

Some of them, like Quicksort and Merge Sort alongside with Heap Sort are based on the divide and conquer principle and are considered efficient sorting algorithms that achieve a much better time complexity of Θ(n log n)
- therefore, are also suitable for large data sets with billions of elements

Quicksort

it picks an element as a pivot and partitions the array based on the pivot
- How to pick pivot?
  - Always pick the first element as a pivot
  - Always pick the last element as a pivot (implemented below)
  - Pick a random element as a pivot
  - Pick median as a pivot
The partition process is a key process
- Choose x element as pivot
- put x and its position in a sorted array
- then put all smaller elements before the pivot, and all larger elements after the pivot

Quick Sort

Bubble Sort

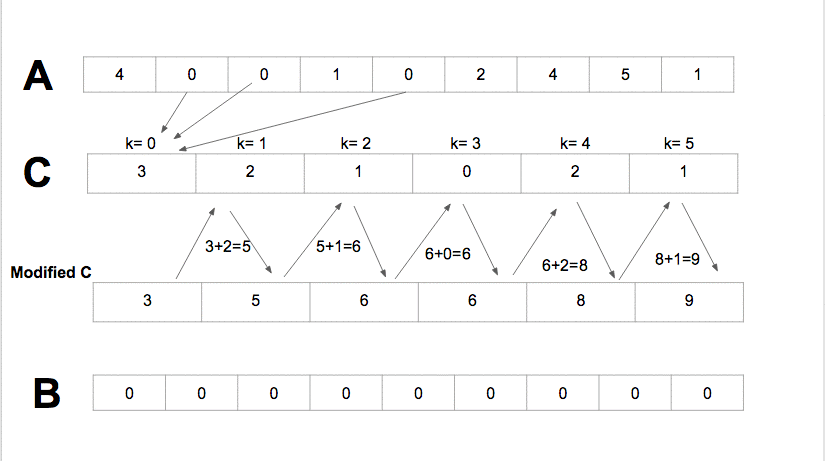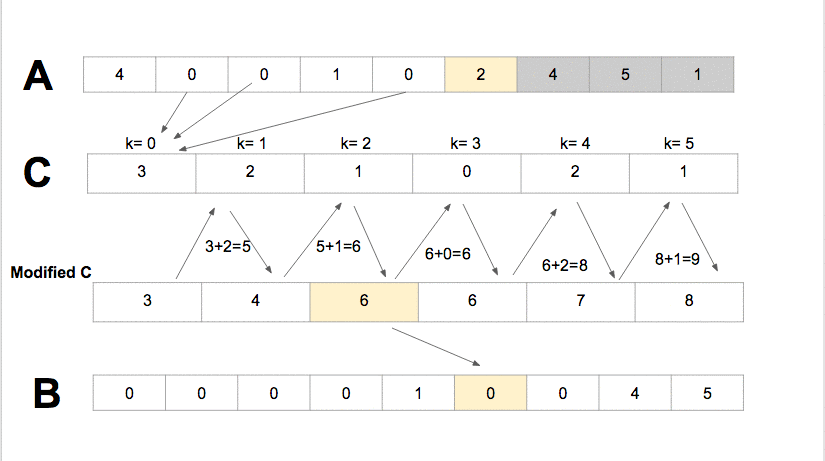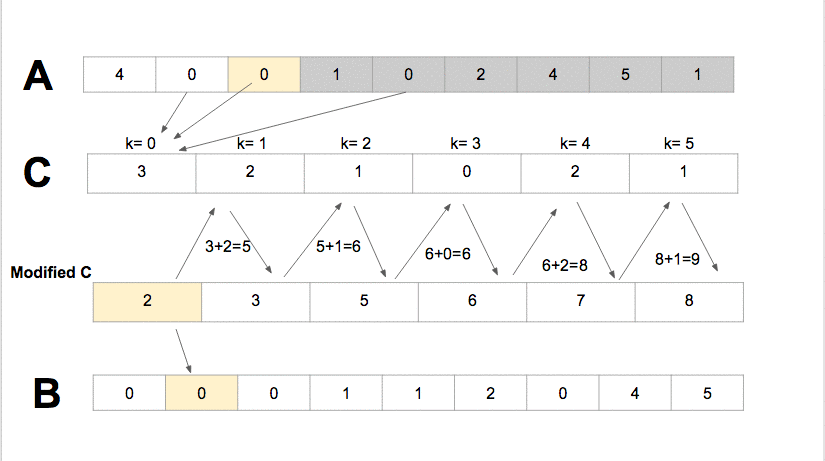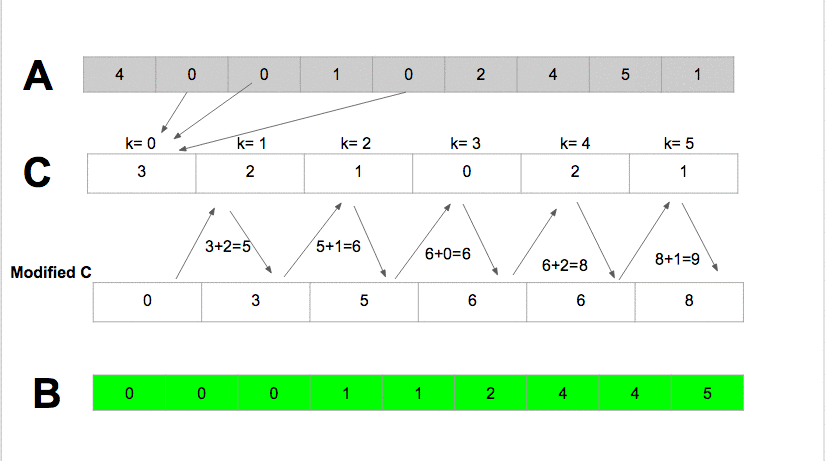
it sorts the elements of an array by counting the number of occurrences of each unique element in the array
It has the linear time and will take O(k + n) time to finish
- where k is the value of the max element in the input array
- it is efficient if the range of input data is not significantly greater than the number of elements to be sorted

Counting Sort

it sorts elements by picking a minimum element from an unsorted subarray and putting it at the beginning of the sorted subarray
- considering ascending order

Selection Sort