Merge Sort

• The merge sort algorithm closely follows the divide-and-conquer paradigm

  1. Divide the n-element sequence to be sorted into two subsequences of n/2 elements each
  2. Conquer: Sort the two subsequences recursively using merge sort
  3. Combine: Merge the two sorted subsequences to produce the sorted answer

  

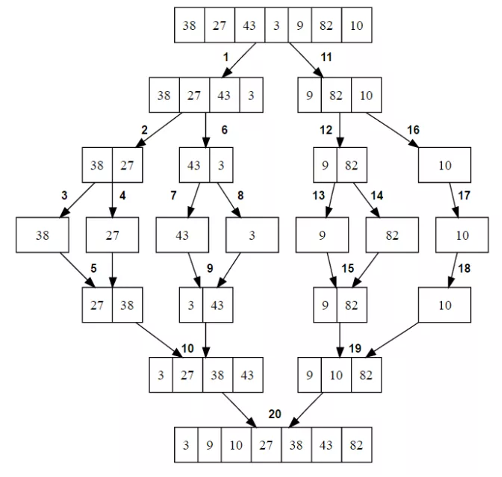
• example

  • We take half the length of the array and divide it into two parts
    • And we call the merge function to the same sorting from the left and right sides
    • The merge function itself compares and merges our sequences
  • Although the code for merge sort works correctly when the number of elements is not even, our recurrence-based analysis is simplified if we assume that the original problem size is a power of 2
    • Each divide step then yields two subsequences of size exactly n/2
    • This assumption does not affect the order of growth of the solution to the recurrence
  • We reason is to set up the recurrence for T(n), the worst-case running time of merge sort on n numbers
    • Merge sort on just one element takes constant time
    • When we have n > 1 elements, we break down the running time as follows:
      • Divide: The divide step just computes the middle of the subarray, which takes constant time
        • Thus, D(n) = Θ(1)
      • Conquer: We recursively solve two subproblems, each of size n/2, which contributes 2T(n/2) to the running time
      • Combine: We have already noted that the MERGE procedure on an n-element subarray takes time Θ(n), and so C(n) = Θ(n)

  function merge(left: number[], right: number[]) {
    const result = [];
    const leftLength = left.length;
    const rightLength = right.length;
    let leftIndex = 0;
    let rightIndex = 0;
  
    while (leftIndex < leftLength && rightIndex < rightLength) {
      if (left[leftIndex] < right[rightIndex]) {
        result.push(left[leftIndex++]);
      } else {
        result.push(right[rightIndex++]);
      }
    }
  
    while (leftIndex < leftLength) {
      result.push(left[leftIndex++]);
    }
  
    while (rightIndex < rightLength) {
      result.push(right[rightIndex++]);
    }
  
    return result;
  }
  
  function mergeSort(numbers: number[]): number[] {
    const length = numbers.length;
    const mid = Math.floor(length * 0.5);
    const left = numbers.slice(0, mid);
    const right = numbers.slice(mid, length);
  
    if (length === 1) {
      return numbers;
    }
  
    return merge(mergeSort(left), mergeSort(right));
  }
  
  console.log(mergeSort([1, 600, 199, 20, 7, 6, 8, 1300, 12, 601]));